| Date | None Specimen | Marks available | 5 | Reference code | SPNone.2.sl.TZ0.7 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 7 | Adapted from | N/A |
Question
A circle centre O and radius \(r\) is shown below. The chord [AB] divides the area of the circle into two parts. Angle AOB is \(\theta \) .
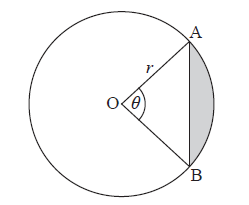
Find an expression for the area of the shaded region.
The chord [AB] divides the area of the circle in the ratio 1:7. Find the value of \(\theta \) .
Markscheme
substitution into formula for area of triangle A1
e.g. \(\frac{1}{2}r \times r\sin \theta \)
evidence of subtraction M1
correct expression A1 N2
e.g. \(\frac{1}{2}{r^2}\theta - \frac{1}{2}{r^2}\sin \theta \) , \(\frac{1}{2}{r^2}(\theta - \sin \theta )\)
[3 marks]
evidence of recognizing that shaded area is \(\frac{1}{8}\) of area of circle M1
e.g. \(\frac{1}{8}\) seen anywhere
setting up correct equation A1
e.g. \(\frac{1}{2}{r^2}(\theta - \sin \theta ) = \frac{1}{8}\pi {r^2}\)
eliminating 1 variable M1
e.g. \(\frac{1}{2}(\theta - \sin \theta ) = \frac{1}{8}\pi \) , \(\theta - \sin \theta = \frac{\pi }{4}\)
attempt to solve M1
e.g. a sketch, writing \(\sin x - x + \frac{\pi }{4} = 0\)
\(\theta = 1.77\) (do not accept degrees) A1 N1
[5 marks]

