| Date | May 2016 | Marks available | 1 | Reference code | 16M.1.hl.TZ1.5 |
| Level | HL only | Paper | 1 | Time zone | TZ1 |
| Command term | Expand | Question number | 5 | Adapted from | N/A |
Question
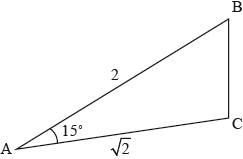
The following diagram shows the triangle ABC where \({\text{AB}} = 2,{\text{ AC}} = \sqrt 2 \) and \({\rm{B\hat AC}} = 15^\circ \).
Expand and simplify \({\left( {1 - \sqrt 3 } \right)^2}\).
By writing \(15^\circ \) as \(60^\circ - 45^\circ \) find the value of \(\cos (15^\circ )\).
Find BC in the form \(a + \sqrt b \) where \(a,{\text{ }}b \in \mathbb{Z}\).
Markscheme
\({\left( {1 - \sqrt 3 } \right)^2} = 4 - 2\sqrt 3 \) A1
Note: Award A0 for \(1 - 2\sqrt 3 + 3\).
[1 mark]
\(\cos (60^\circ - 45^\circ ) = \cos (60^\circ )\cos (45^\circ ) + \sin (60^\circ )\sin (45^\circ )\) M1
\( = \frac{1}{2} \times \frac{{\sqrt 2 }}{2} + \frac{{\sqrt 3 }}{2} \times \frac{{\sqrt 2 }}{2}{\text{ }}\left( {{\text{or }}\frac{1}{2} \times \frac{1}{{\sqrt 2 }} + \frac{{\sqrt 3 }}{2} \times \frac{1}{{\sqrt 2 }}} \right)\) (A1)
\( = \frac{{\sqrt 2 + \sqrt 6 }}{4}{\text{ }}\left( {{\text{or }}\frac{{1 + \sqrt 3 }}{{2\sqrt 2 }}} \right)\) A1
[3 marks]
\(B{C^2} = 2 + 4 - 2 \times \sqrt 2 \times 2\cos (15^\circ )\) M1
\( = 6 - \sqrt 2 \left( {\sqrt 2 + \sqrt 6 } \right)\)
\( = 4 - \sqrt {12} {\text{ }}\left( { = 4 - 2\sqrt 3 } \right)\) A1
\(BC = \pm \left( {1 - \sqrt 3 } \right)\) (M1)
\(BC = - 1 + \sqrt 3 \) A1
Note: Accept \(BC = \sqrt 3 - 1\).
Note: Award M1A0 for \(1 - \sqrt 3 \).
Note: Valid geometrical methods may be seen.
[4 marks]
Examiners report
The main error here was to fail to note the word ‘simplify’ in the question and some candidates wrote \(1 + 3\) in their final answer rather than 4.
This was well done by the majority of candidates, though a few wrote \(\cos (60 - 45) = \cos 60 - \cos 45\).
Candidates were able to use the cosine rule correctly but then failed to notice the result obtained was the same as that obtained in part (a).

