| Date | May 2015 | Marks available | 6 | Reference code | 15M.2.hl.TZ1.4 |
| Level | HL only | Paper | 2 | Time zone | TZ1 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
A triangle \(ABC\) has \(\hat A = 50^\circ \), \({\text{AB}} = 7{\text{ cm}}\) and \({\text{BC}} = 6{\text{ cm}}\). Find the area of the triangle given that it is smaller than \(10{\text{ c}}{{\text{m}}^2}\).
Markscheme
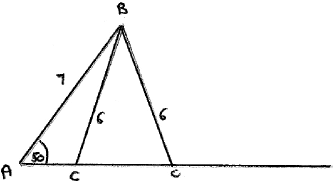
METHOD 1
\(\frac{6}{{\sin 50}} = \frac{7}{{\sin C}} \Rightarrow \sin C = \frac{{7\sin 50}}{6}\) (M1)
\(C = 63.344 \ldots \) (A1)
or\(\;\;\;C = 116.655 \ldots \) (A1)
\(B = 13.344 \ldots \;\;\;({\text{or }}B = 66.656 \ldots )\) (A1)
\({\text{area}} = \frac{1}{2} \times 6 \times 7 \times \sin 13.344 \ldots \;\;\;\left( {{\text{or }}\frac{1}{2} \times 6 \times 7 \times \sin 66.656 \ldots } \right)\) (M1)
\(4.846 \ldots \;\;\;({\text{or }} = 19.281 \ldots )\)
so answer is \(4.85{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1
METHOD 2
\({6^2} = {7^2} + {b^2} - 2 \times 7b\cos 50\) (M1)(A1)
\({b^2} - 14b\cos 50 + 13 = 0\;\;\;\)or equivalent method to solve the above equation (M1)
\(b = 7.1912821 \ldots \;\;\;{\text{or}}\;\;\;b = 1.807744 \ldots \) (A1)
\({\text{area}} = \frac{1}{2} \times 7 \times 1.8077 \ldots \sin 50 = 4.846 \ldots \) (M1)
\(\left( {{\text{or }}\frac{1}{2} \times 7 \times 7.1912821 \ldots \sin 50 = 19.281 \ldots } \right)\)
so answer is \(4.85{\text{ (c}}{{\text{m}}^2}{\text{)}}\) A1
METHOD 3
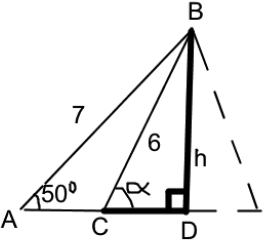
Diagram showing triangles \(ACB\) and \(ADB\) (M1)
\(h = 7\sin (50) = 5.3623 \ldots {\text{ (cm)}}\) (M1)
\(\alpha = \arcsin \frac{h}{6} = 63.3442 \ldots \) (M1)
\({\text{AC}} = {\text{AD}} - {\text{CD}} = 7\cos 50 - 6\cos \alpha = 1.8077 \ldots {\text{ (cm)}}\) (M1)
\({\text{area}} = \frac{1}{2} \times 1.8077 \ldots \times 5.3623 \ldots \) (M1)
\( = 4.85{\text{ (c}}{{\text{m}}^{\text{2}}}{\text{)}}\) A1
Total [6 marks]
Examiners report
Most candidates scored 4/6 showing that candidates do not have enough experience with the ambiguous case. Very few candidates drew a suitable diagram that would have illustrated this fact which could have helped them to understand the requirement that the answer should be less than 10. In fact many candidates ignored this requirement or used it incorrectly to solve an inequality.

