| Date | May 2008 | Marks available | 12 | Reference code | 08M.2.hl.TZ1.12 |
| Level | HL only | Paper | 2 | Time zone | TZ1 |
| Command term | Prove, Show that, and Hence | Question number | 12 | Adapted from | N/A |
Question
In triangle ABC, BC = a , AC = b , AB = c and [BD] is perpendicular to [AC].
(a) Show that \({\text{CD}} = b - c\cos A\).
(b) Hence, by using Pythagoras’ Theorem in the triangle BCD, prove the cosine rule for the triangle ABC.
(c) If \({\rm{A\hat BC}} = 60^\circ \) , use the cosine rule to show that \(c = \frac{1}{2}a \pm \sqrt {{b^2} - \frac{3}{4}{a^2}} \) .
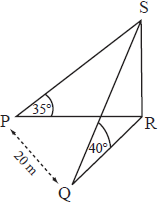
The above three dimensional diagram shows the points P and Q which are respectively west and south-west of the base R of a vertical flagpole RS on horizontal ground. The angles of elevation of the top S of the flagpole from P and Q are respectively 25° and 40° , and PQ = 20 m .
Determine the height of the flagpole.
Markscheme
(a) \({\text{CD}} = {\text{AC}} - {\text{AD}} = b - c\cos A\) R1AG
[1 mark]
(b) METHOD 1
\({\text{B}}{{\text{C}}^2} = {\text{B}}{{\text{D}}^2} + {\text{C}}{{\text{D}}^2}\) (M1)
\({a^2} = {(c\sin A)^2} + {(b - c\cos A)^2}\) (A1)
\( = {c^2}{\sin ^2}A + {b^2} - 2bc\cos A + {c^2}{\cos ^2}A\) A1
\( = {b^2} + {c^2} - 2bc\cos A\) A1
[4 marks]
METHOD 2
\({\text{B}}{{\text{D}}^2} = {\text{A}}{{\text{B}}^2} - {\text{A}}{{\text{D}}^2} = {\text{B}}{{\text{C}}^2} - {\text{C}}{{\text{D}}^2}\) (M1)(A1)
\( \Rightarrow {c^2} - {c^2}{\cos ^2}A = {a^2} - {b^2} + 2bc\cos A - {c^2}{\cos ^2}A\) A1
\( \Rightarrow {a^2} = {b^2} + {c^2} - 2bc\cos A\) A1
[4 marks]
(c) METHOD 1
\({b^2} = {a^2} + {c^2} - 2ac\cos 60^\circ \Rightarrow {b^2} = {a^2} + {c^2} - ac\) (M1)A1
\( \Rightarrow {c^2} - ac + {a^2} - {b^2} = 0\) M1
\( \Rightarrow c = \frac{{a \pm \sqrt {{{( - a)}^2} - 4({a^2} - {b^2})} }}{2}\) (M1)A1
\( = \frac{{a \pm \sqrt {4{b^2} - 3{a^2}} }}{2} = \frac{a}{2} \pm \sqrt {\frac{{4{b^2} - 3{a^2}}}{4}} \) (M1)A1
\( = \frac{1}{2}a \pm \sqrt {{b^2} - \frac{3}{4}{a^2}} \) AG
Note: Candidates can only obtain a maximum of the first three marks if they verify that the answer given in the question satisfies the equation.
[7 marks]
METHOD 2
\({b^2} = {a^2} + {c^2} - 2ac\cos 60^\circ \Rightarrow {b^2} = {a^2} + {c^2} - ac\) (M1)A1
\({c^2} - ac = {b^2} - {a^2}\) (M1)
\({c^2} - ac + {\left( {\frac{a}{2}} \right)^2} = {b^2} - {a^2} + {\left( {\frac{a}{2}} \right)^2}\) M1A1
\({\left( {c - \frac{a}{2}} \right)^2} = {b^2} - \frac{3}{4}{a^2}\) (A1)
\(c - \frac{a}{2} = \pm \sqrt {{b^2} - \frac{3}{4}{a^2}} \) A1
\( \Rightarrow c = \frac{1}{2}a \pm \sqrt {{b^2} - \frac{3}{4}{a^2}} \) AG
[7 marks]
\({\text{PR}} = h\tan 55^\circ {\text{ , QR}} = h\tan 50^\circ {\text{ where RS}} = h\) M1A1A1
Use the cosine rule in triangle PQR. (M1)
\({20^2} = {h^2}{\tan ^2}55^\circ + {h^2}{\tan ^2}50^\circ - 2h\tan 55^\circ h\tan 50^\circ \cos 45^\circ \) A1
\({h^2} = \frac{{400}}{{{{\tan }^2}55^\circ + {{\tan }^2}50^\circ - 2\tan 55^\circ \tan 50^\circ \cos 45^\circ }}\) (A1)
\( = 379.9…\) (A1)
\(h = 19.5{\text{ (m)}}\) A1
[8 marks]
Examiners report
The majority of the candidates attempted part A of this question. Parts (a) and (b) were answered reasonably well. In part (c), many candidates scored the first two marks, but failed to recognize that the result was a quadratic equation, and hence did not progress further.
Correct answers to part B were rarely seen. Although many candidates expressed RS correctly in two different ways, they failed to go on to use the cosine rule.

