| Date | November 2017 | Marks available | 6 | Reference code | 17N.2.hl.TZ0.5 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 5 | Adapted from | N/A |
Question
Barry is at the top of a cliff, standing 80 m above sea level, and observes two yachts in the sea.
“Seaview” \((S)\) is at an angle of depression of 25°.
“Nauti Buoy” \((N)\) is at an angle of depression of 35°.
The following three dimensional diagram shows Barry and the two yachts at S and N.
X lies at the foot of the cliff and angle \({\text{SXN}} = \) 70°.
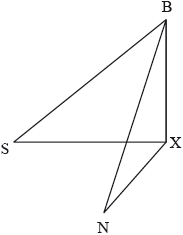
Find, to 3 significant figures, the distance between the two yachts.
Markscheme
attempt to use tan, or sine rule, in triangle BXN or BXS (M1)
\({\text{NX}} = 80\tan 55{\rm{^\circ }}\left( { = \frac{{80}}{{\tan 35{\rm{^\circ }}}} = 114.25} \right)\) (A1)
\({\text{SX}} = 80\tan 65{\rm{^\circ }}\left( { = \frac{{80}}{{\tan 25{\rm{^\circ }}}} = 171.56} \right)\) (A1)
Attempt to use cosine rule M1
\({\text{S}}{{\text{N}}^2} = {171.56^2} + {114.25^2} - 2 \times 171.56 \times 114.25\cos 70\)° (A1)
\({\text{SN}} = 171{\text{ }}({\text{m}})\) A1
Note: Award final A1 only if the correct answer has been given to 3 significant figures.
[6 marks]

