| Date | May 2014 | Marks available | 3 | Reference code | 14M.2.sl.TZ2.5 |
| Level | SL | Paper | 2 | Time zone | TZ2 |
| Command term | Calculate | Question number | 5 | Adapted from | N/A |
Question
A group of students investigated the rate of the reaction between aqueous sodium thiosulfate and hydrochloric acid according to the equation below.
\[{\text{N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3}{\text{(aq)}} + {\text{2HCl(aq)}} \to {\text{2NaCl(aq)}} + {\text{S}}{{\text{O}}_2}{\text{(g)}} + {\text{S(s)}} + {{\text{H}}_2}{\text{O(l)}}\]
The two reagents were rapidly mixed together in a beaker and placed over a mark on a piece of paper. The time taken for the precipitate of sulfur to obscure the mark when viewed through the reaction mixture was recorded.
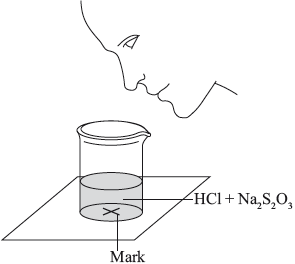
Initially they measured out \({\text{10.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) hydrochloric acid and then added \({\text{40.0 c}}{{\text{m}}^{\text{3}}}\) of \({\text{0.0200 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) aqueous sodium thiosulfate. The mark on the paper was obscured 47 seconds after the solutions were mixed.
The teacher asked the students to measure the effect of halving the concentration of sodium thiosulfate on the rate of reaction.
The teacher asked the students to devise another technique to measure the rate of this reaction.
Another group suggested collecting the sulfur dioxide and drawing a graph of the volume of gas against time.
The teacher made up \({\text{2.50 d}}{{\text{m}}^{\text{3}}}\) of the sodium thiosulfate solution using sodium thiosulfate pentahydrate crystals, \({\text{N}}{{\text{a}}_2}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}} \bullet {\text{5}}{{\text{H}}_{\text{2}}}{\text{O}}\). Calculate the required mass of these crystals.
(i) State the volumes of the liquids that should be mixed.

(ii) State why it is important that the students use a similar beaker for both reactions.
(iii) Explain, in terms of the collision theory, how decreasing the concentration of sodium thiosulfate would affect the time taken for the mark to be obscured.
(i) Sketch and label, indicating an approximate activation energy, the Maxwell–Boltzmann energy distribution curves for two temperatures, \({T_1}\) and \({T_2}{\text{ }}({T_2} > {T_1})\), at which the rate of reaction would be significantly different.

(ii) Explain why increasing the temperature of the reaction mixture would significantly increase the rate of the reaction.
(i) One group suggested recording how long it takes for the pH of the solution to change by one unit. Calculate the initial pH of the original reaction mixture.
(ii) Deduce the percentage of hydrochloric acid that would have to be used up for the pH to change by one unit.
(i) Calculate the volume of sulfur dioxide, in \({\text{c}}{{\text{m}}^{\text{3}}}\), that the original reaction mixture would produce if it were collected at \(1.00 \times {10^5}{\text{ Pa}}\) and 300 K.
(ii) Suggest why it is better to use a gas syringe rather than collecting the gas in a measuring cylinder over water.
Markscheme
\({\text{mol N}}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}( = 2.50 \times 0.0200) = 0.0500\);
\({{\text{M}}_{\text{r}}}{\text{N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3} \bullet {\text{5}}{{\text{H}}_2}{\text{O}}\left( { = (2 \times 22.99) + (2 \times 32.06) + (3 \times 16.00) + (5 \times 18.02)} \right) = 248.20\);
Allow 248.
\({\text{mass N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3} \bullet {\text{5}}{{\text{H}}_2}{\text{O}} = (0.0500 \times 248.20) = 12.4{\text{ g}}\);
Award [3] for correct final answer.
Award [2] for 7.91g (water of crystallization omitted in \({M_r}\) calculation).
(i)  ;
;
Accept other volumes in a 1:2:2 ratio.
(ii) depth of liquid in the beaker must remain constant / OWTTE;
Accept “same thickness of glass” and any other valid point, such as answers framed around minimizing uncontrolled variables / making it a “fair test”.
(iii) increases the time;
decrease in collision frequency/number of collisions per unit time;
Do not award mark for decrease in number of collisions.
(i) 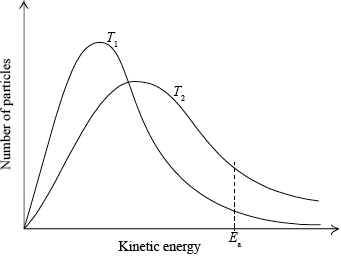
labelled y-axis: number of particles / probability of particles (with that kinetic energy) and labelled x-axis: (kinetic) energy;
Allow fraction/proportion/amount of particles (with kinetic energy) for y-axis label.
Allow speed/velocity for x-axis label.
T2 curve broader and with maximum lower and to right of T1 curve;
Do not award this mark if both curves not asymmetric.
Curves must pass through the origin and be asymptotic to x axis.
Do not award this mark if curves not labelled.
\({E_{\text{a}}}\) marked on graph;
(ii) kinetic energy of molecules increases;
This may be answered implicitly in the final marking point.
frequency of collision/number of collisions per unit time increases;
Only penalize use of “number of collisions” if not penalized in (b)(iii).
greater proportion of molecules have energy greater than/equal to activation energy / rate related to temperature by the Arrhenius equation;
Award [1 max] for statements such as “there will be more successful collisions” if neither of last two marking points awarded.
(i) \({\text{[}}{{\text{H}}^ + }{\text{]}} = 0.5 \times \frac{{10}}{{{\text{50}}}} = 0.1{\text{ (mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{)}}\);
\({\text{pH }}\left( { = - \log {\text{[}}{{\text{H}}^ + }{\text{]}} = - \log (0.10)} \right) = 1\);
(ii) 90%;
(i) \({\text{mol N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3} = {\text{mol S}}{{\text{O}}_2} = 0.0400 \times 0.0200 = 0.000800\);
\(V = \frac{{n \times R \times T}}{P}/\frac{{0.000800 \times 8.31 \times 300}}{{{{10}^5}}}\);
\((1.99 \times {10^{ - 5}}{\text{ }}{{\text{m}}^3}) = 19.9{\text{ }}({\text{c}}{{\text{m}}^3})\);
Award [3] for correct final answer.
Accept 20.0 cm3 if R = 8.314 is used.
Award [2] for 17.9 cm3 or 19.2 cm3 (result from using molar volume at standard temperature and pressure or at room temperature and pressure).
OR
\({\text{mol N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3} = {\text{mol S}}{{\text{O}}_2} = 0.0400 \times 0.0200 = 0.000800\);
\(V = 0.00080 \times 2.24 \times {10^{ - 2}} \times \left[ {\frac{{1.00 \times {{10}^5}}}{{1.01 \times {{10}^5}}}} \right] \times \frac{{300}}{{273}}\);
\((1.95 \times {10^{ - 5}}{\text{ }}{{\text{m}}^3}) = 19.5{\text{ }}({\text{c}}{{\text{m}}^3})\);
Award [3] for correct final answer.
Deduct [1] for answers based on amount of HCl, so correct calculation would score [2 max].
(ii) sulfur dioxide is soluble in water;
Accept other reasonable responses based on sound chemistry.
Accept “syringe more accurate/precise” or “less gas escapes”.
Examiners report
This was quite a popular question, but responses were mixed. As in question 1, students struggled to answer questions with a strong practical context, with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and responses for the need for similar beakers to be used were often too vague. Explanations of changes of rates in terms of the collision theory were generally successful but a significant number referred to the “number” rather than “frequency” of collisions. Many candidates were able to sketch Maxwell–Boltzmann distribution curves for the two temperatures, \({T_1}\) and \({T_2}\), but marks were lost due to careless omissions; the graphs did not start at the origin, were not labelled or the activation energy was missing. Many struggled to calculate the pH and many teachers have commented that this question was beyond what is expected at Standard Level and it is acknowledged that the question would have been more accessible if candidates had been asked to calculate the concentration of \({{\text{H}}^ + }\) ions and state the pH. In part (e) many students could quote and substitute into the ideal gas equation, correctly converting the temperature to Kelvin, but converting from \({{\text{m}}^{\text{3}}}\) to \({\text{c}}{{\text{m}}^{\text{3}}}\) posed a problem for most candidates. Although not necessary for the mark, as answers which referred to improved accuracy and precision were accepted, most candidates did not refer to the solubility of sulfur dioxide as a problem when using measuring cylinders to measure its volume.
This was quite a popular question, but responses were mixed. As in question 1, students struggled to answer questions with a strong practical context, with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and responses for the need for similar beakers to be used were often too vague. Explanations of changes of rates in terms of the collision theory were generally successful but a significant number referred to the “number” rather than “frequency” of collisions. Many candidates were able to sketch Maxwell–Boltzmann distribution curves for the two temperatures, \({T_1}\) and \({T_2}\), but marks were lost due to careless omissions; the graphs did not start at the origin, were not labelled or the activation energy was missing. Many struggled to calculate the pH and many teachers have commented that this question was beyond what is expected at Standard Level and it is acknowledged that the question would have been more accessible if candidates had been asked to calculate the concentration of \({{\text{H}}^ + }\) ions and state the pH. In part (e) many students could quote and substitute into the ideal gas equation, correctly converting the temperature to Kelvin, but converting from \({{\text{m}}^{\text{3}}}\) to \({\text{c}}{{\text{m}}^{\text{3}}}\) posed a problem for most candidates. Although not necessary for the mark, as answers which referred to improved accuracy and precision were accepted, most candidates did not refer to the solubility of sulfur dioxide as a problem when using measuring cylinders to measure its volume.
This was quite a popular question, but responses were mixed. As in question 1, students struggled to answer questions with a strong practical context, with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and responses for the need for similar beakers to be used were often too vague. Explanations of changes of rates in terms of the collision theory were generally successful but a significant number referred to the “number” rather than “frequency” of collisions. Many candidates were able to sketch Maxwell–Boltzmann distribution curves for the two temperatures, \({T_1}\) and \({T_2}\), but marks were lost due to careless omissions; the graphs did not start at the origin, were not labelled or the activation energy was missing. Many struggled to calculate the pH and many teachers have commented that this question was beyond what is expected at Standard Level and it is acknowledged that the question would have been more accessible if candidates had been asked to calculate the concentration of \({{\text{H}}^ + }\) ions and state the pH. In part (e) many students could quote and substitute into the ideal gas equation, correctly converting the temperature to Kelvin, but converting from \({{\text{m}}^{\text{3}}}\) to \({\text{c}}{{\text{m}}^{\text{3}}}\) posed a problem for most candidates. Although not necessary for the mark, as answers which referred to improved accuracy and precision were accepted, most candidates did not refer to the solubility of sulfur dioxide as a problem when using measuring cylinders to measure its volume.
This was quite a popular question, but responses were mixed. As in question 1, students struggled to answer questions with a strong practical context, with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and responses for the need for similar beakers to be used were often too vague. Explanations of changes of rates in terms of the collision theory were generally successful but a significant number referred to the “number” rather than “frequency” of collisions. Many candidates were able to sketch Maxwell–Boltzmann distribution curves for the two temperatures, \({T_1}\) and \({T_2}\), but marks were lost due to careless omissions; the graphs did not start at the origin, were not labelled or the activation energy was missing. Many struggled to calculate the pH and many teachers have commented that this question was beyond what is expected at Standard Level and it is acknowledged that the question would have been more accessible if candidates had been asked to calculate the concentration of \({{\text{H}}^ + }\) ions and state the pH. In part (e) many students could quote and substitute into the ideal gas equation, correctly converting the temperature to Kelvin, but converting from \({{\text{m}}^{\text{3}}}\) to \({\text{c}}{{\text{m}}^{\text{3}}}\) posed a problem for most candidates. Although not necessary for the mark, as answers which referred to improved accuracy and precision were accepted, most candidates did not refer to the solubility of sulfur dioxide as a problem when using measuring cylinders to measure its volume.
This was quite a popular question, but responses were mixed. As in question 1, students struggled to answer questions with a strong practical context, with very few able to devise a mixture that would halve the concentration of thiosulfate, whilst keeping other concentrations constant, and responses for the need for similar beakers to be used were often too vague. Explanations of changes of rates in terms of the collision theory were generally successful but a significant number referred to the “number” rather than “frequency” of collisions. Many candidates were able to sketch Maxwell–Boltzmann distribution curves for the two temperatures, \({T_1}\) and \({T_2}\), but marks were lost due to careless omissions; the graphs did not start at the origin, were not labelled or the activation energy was missing. Many struggled to calculate the pH and many teachers have commented that this question was beyond what is expected at Standard Level and it is acknowledged that the question would have been more accessible if candidates had been asked to calculate the concentration of \({{\text{H}}^ + }\) ions and state the pH. In part (e) many students could quote and substitute into the ideal gas equation, correctly converting the temperature to Kelvin, but converting from \({{\text{m}}^{\text{3}}}\) to \({\text{c}}{{\text{m}}^{\text{3}}}\) posed a problem for most candidates. Although not necessary for the mark, as answers which referred to improved accuracy and precision were accepted, most candidates did not refer to the solubility of sulfur dioxide as a problem when using measuring cylinders to measure its volume.

