| Date | November 2012 | Marks available | 6 | Reference code | 12N.2.sl.TZ0.1 |
| Level | SL | Paper | 2 | Time zone | TZ0 |
| Command term | Calculate, Determine, and State | Question number | 1 | Adapted from | N/A |
Question
Two groups of students (Group A and Group B) carried out a project* on the chemistry of some group 7 elements (the halogens) and their compounds.
* Adapted from J Derek Woollins, (2009), Inorganic Experiments and Open University, (2008), Exploring the Molecular World.
In the first part of the project, the two groups had a sample of iodine monochloride (a corrosive brown liquid) prepared for them by their teacher using the following reaction.
\[{{\text{I}}_{\text{2}}}{\text{(s)}} + {\text{C}}{{\text{l}}_{\text{2}}}{\text{(g)}} \to {\text{2ICl(l)}}\]
The following data were recorded.
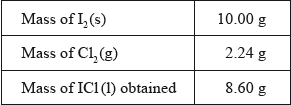
The students reacted ICl(l) with CsBr(s) to form a yellow solid, \({\text{CsIC}}{{\text{l}}_{\text{2}}}{\text{(s)}}\), as one of the products. \({\text{CsIC}}{{\text{l}}_{\text{2}}}{\text{(s)}}\) has been found to produce very pure CsCl(s) which is used in cancer treatment.
To confirm the composition of the yellow solid, Group A determined the amount of iodine in 0.2015 g of \({\text{CsIC}}{{\text{l}}_{\text{2}}}{\text{(s)}}\) by titrating it with \({\text{0.0500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ N}}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\). The following data were recorded for the titration.

(i) State the number of significant figures for the masses of \({{\text{I}}_{\text{2}}}{\text{(s)}}\) and ICl(l).
\({{\text{I}}_{\text{2}}}{\text{(s)}}\):
ICl (l):
(ii) The iodine used in the reaction was in excess. Determine the theoretical yield, in g, of ICl(l).
(iii) Calculate the percentage yield of ICl(l).
(iv) Using a digital thermometer, the students discovered that the reaction was exothermic. State the sign of the enthalpy change of the reaction, \(\Delta H\).
Although the molar masses of ICl and \({\rm{B}}{{\rm{r}}_2}\) are very similar, the boiling point of ICl is 97.4 °C and that of \({\rm{B}}{{\rm{r}}_2}\) is 58.8 °C. Explain the difference in these boiling points in terms of the intermolecular forces present in each liquid.
(i) Calculate the percentage of iodine by mass in \({\text{CsIC}}{{\text{l}}_{\text{2}}}{\text{(s)}}\), correct to three significant figures.
(ii) State the volume, in \({\text{c}}{{\text{m}}^{\text{3}}}\), of \({\text{0.0500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ N}}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\) used in the titration.
(iii) Determine the amount, in mol, of \({\text{0.0500 mol}}\,{\text{d}}{{\text{m}}^{ - 3}}{\text{ N}}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\) added in the titration.
(iv) The overall reaction taking place during the titration is:
\[{\text{CsICl(s)}} + {\text{2N}}{{\text{a}}_2}{{\text{S}}_2}{{\text{O}}_3}{\text{(aq)}} \to {\text{NaCl(aq)}} + {\text{N}}{{\text{a}}_2}{{\text{S}}_4}{{\text{O}}_6}{\text{(aq)}} + {\text{CsCl(aq)}} + {\text{NaI(aq)}}\]
Calculate the amount, in mol, of iodine atoms, I, present in the sample of \({\text{CsIC}}{{\text{l}}_{\text{2}}}{\text{(s)}}\).
(v) Calculate the mass of iodine, in g, present in the sample of \({\text{CsIC}}{{\text{l}}_{\text{2}}}\)
(vi) Determine the percentage by mass of iodine in the sample of \({\text{CsIC}}{{\text{l}}_{\text{2}}}{\text{(s)}}\), correct to three significant figures, using your answer from (v).
Markscheme
(i) I2(s): four/4 and ICl(l): three/3;
(ii) \(n{\text{(C}}{{\text{l}}_2}{\text{)}} = {\text{ }}\left( {\frac{{2.24}}{{2 \times 35.45}} = } \right){\text{ }}0.0316/3.16 \times {10^{ - 2}}{\text{ (mol)}}\);
Allow answers such as 3.2 \( \times \) 10–2/0.032/3.15 \( \times \) 10–2/0.0315 (mol).
\(n{\text{(ICl)}} = 2 \times 0.0316/0.0632/6.32 \times {10^{ - 2}}{\text{ (mol)}}\);
Allow answers such as 6.4 \( \times \) 10–2/0.064/6.3 \( \times \) 10–2/0.063 (mol).
\(m{\text{(ICl)}} = (0.0632 \times 162.35 = ){\text{ }}10.3{\text{ (g)}}\);
Allow answers in range 10.2 to 10.4 (g).
Award [3] for correct final answer.
(iii) \(\left( {\frac{{8.60}}{{10.3}} \times 100 = } \right){\text{ }}83.5\% \);
Allow answers in the range of 82.5 to 84.5%.
(iv) negative/–/minus/ < 0;
Br2 has London/dispersion/van der Waals’ forces/vdW and ICl has (London/dispersion/van der Waals’ forces/vdW and) dipole–dipole forces;
dipole–dipole forces are stronger than London/dispersion/van der Waals’/vdW forces;
Allow induced dipole-induced dipole forces for London forces.
Allow interactions instead of forces.
Do not allow ICl polar and Br2 non-polar for M1.
Name of IMF in both molecules is required for M1 and idea of dipole-dipole stronger than vdW is required for M2.
(i) \(\left( {\frac{{126.90}}{{330.71}} \times 100} \right) = 38.4\% \);
(ii) \((25.25 - 1.05) = 24.20{\text{ (c}}{{\text{m}}^{\text{3}}}{\text{)}}\);
Accept 24.2 (cm3) but not 24 (cm3).
(iii) \(\left( {\frac{{24.20 \times 5.00 \times {{10}^{ - 2}}}}{{1000}}} \right) = 1.21 \times {10^{ - 3}}/0.00121{\text{ (mol)}}\);
(iv) \((0.5 \times 1.21 \times {10^{ - 3}}) = 6.05 \times {10^{ - 4}}/0.000605{\text{ (mol)}}\);
Accept alternate method e.g. (0.384/126.9 \( \times \) 0.2015) = 6.10 \( \times \) 10–4/0.000610 (mol).
(v) \((126.90 \times 6.05 \times {10^{ - 4}}) = 7.68 \times {10^{ - 2}}/0.0768{\text{ (g)}}\);
Accept alternate method e.g. (6.10 \( \times \) 10–4 \( \times \) 126.9) or (0.2015 \( \times \) 0.384) = 7.74 \( \times \) 10–2/0.00774 (g).
(vi) \(\left( {\frac{{7.68 \times {{10}^{ - 2}}}}{{0.2015}} \times 100} \right) = 38.1\% \);
Answer must be given to three significant figures.
Examiners report
This was a data based question based on quantitative chemistry. Majority of candidates were able to gain almost full marks with some candidates failing to recognise that chlorine is the limiting reagent in part (a) (ii). Some candidates calculated percentage experimental error instead of percentage yield whereas some other candidates did not pay attention to significant digits.
In part (b), explaining the difference in the boiling points of Br2 and ICl in terms of the intermolecular forces presented a challenge to many candidates. Explanations were vague or unclear and in some cases incorrect in terms of the intermolecular forces present.
In part (c), calculations of moles of iodine occasionally saw the erroneous use of Avogadro’s constant.

