| Date | May 2017 | Marks available | 2 | Reference code | 17M.2.hl.TZ0.6 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 6 | Adapted from | N/A |
Question
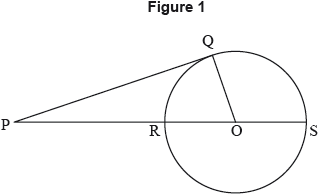
Figure 1 shows a tangent [PQ] at the point Q of a circle and a line [PS] meeting the circle at the points R , S and passing through the centre O of the circle.
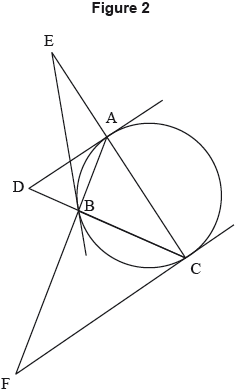
Figure 2 shows a triangle ABC inscribed in a circle. The tangents at the points A , B , C meet the opposite sides of the triangle externally at the points D , E , F respectively.
Show that \({\text{P}}{{\text{Q}}^2} = {\text{PR}} \times {\text{PS}}\).
State briefly how this result can be generalized to give the tangent-secant theorem.
Show that \(\frac{{{\text{A}}{{\text{D}}^2}}}{{{\text{B}}{{\text{D}}^2}}} = \frac{{{\text{CD}}}}{{{\text{BD}}}}\).
By considering a pair of similar triangles, show that
\(\frac{{{\text{AD}}}}{{{\text{BD}}}} = \frac{{{\text{AC}}}}{{{\text{AB}}}}\) and hence that \(\frac{{{\text{CD}}}}{{{\text{BD}}}} = \frac{{{\text{A}}{{\text{C}}^2}}}{{{\text{A}}{{\text{B}}^2}}}\).
By writing down and using two further similar expressions, show that the points D, E, F are collinear.
Markscheme
let \(r = \) radius of circle. Consider
\({\text{PR}} \times {\text{PS}} = ({\text{PO}} - r)({\text{PO}} + r)\) M1
\( = {\text{P}}{{\text{O}}^2} - {\text{O}}{{\text{Q}}^2}\) A1
\( = {\text{P}}{{\text{Q}}^2}\) because POQ is a right angled triangle R1
[2 marks]
the result is true even if PS does not pass through O A1
[2 marks]
using the tangent-secant theorem, M1
\({\text{A}}{{\text{D}}^2} = {\text{BD}} \times {\text{CD}}\) A1
so \(\frac{{{\text{A}}{{\text{D}}^2}}}{{{\text{B}}{{\text{D}}^2}}} = \frac{{{\text{CD}}}}{{{\text{BD}}}} \ldots {\text{ (1)}}\) AG
[??? marks]
consider the triangles CAD and ABD. They are similar because M1
\({\rm{D\hat AB}} = {\rm{A\hat CD}}\), angle \({\rm{\hat D}}\) is common therefore the third angles must be equal A1
Note: Beware of the assumption that AC is a diameter of the circle.
therefore
\(\frac{{{\text{AD}}}}{{{\text{BD}}}} = \frac{{{\text{AC}}}}{{{\text{AB}}}} \ldots {\text{ (2)}}\) AG
it follows from (1) and (2) that
\(\frac{{{\text{CD}}}}{{{\text{BD}}}} = \frac{{{\text{A}}{{\text{C}}^2}}}{{{\text{A}}{{\text{B}}^2}}}\) AG
[??? marks]
two similar expressions are
\(\frac{{{\text{AE}}}}{{{\text{CE}}}} = \frac{{{\text{B}}{{\text{A}}^2}}}{{{\text{B}}{{\text{C}}^2}}}\) M1A1
\(\frac{{{\text{BF}}}}{{{\text{AF}}}} = \frac{{{\text{C}}{{\text{B}}^2}}}{{{\text{C}}{{\text{A}}^2}}}\) A1
multiplying the three expressions,
\(\frac{{{\text{CD}}}}{{{\text{BD}}}} \times \frac{{{\text{AE}}}}{{{\text{CE}}}} \times \frac{{{\text{BF}}}}{{{\text{AF}}}} = \frac{{{\text{A}}{{\text{C}}^2}}}{{{\text{A}}{{\text{B}}^2}}} \times \frac{{{\text{B}}{{\text{A}}^2}}}{{{\text{B}}{{\text{C}}^2}}} \times \frac{{{\text{C}}{{\text{B}}^2}}}{{{\text{C}}{{\text{A}}^2}}}\) M1
\(\frac{{{\text{CD}}}}{{{\text{BD}}}} \times \frac{{{\text{AE}}}}{{{\text{CE}}}} \times \frac{{{\text{BF}}}}{{{\text{AF}}}} = 1\) A1
it follows from the converse of Menelaus’ theorem (ignoring signs) R1
that D, E, F are collinear AG
[??? marks]

