| Date | May 2009 | Marks available | 4 | Reference code | 09M.1.hl.TZ0.3 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Calculate | Question number | 3 | Adapted from | N/A |
Question
Triangle ABC has points D, E and F on sides [BC], [CA] and [AB] respectively; [AD], [BE] and [CF] intersect at the point P. If 3BD = 2DC and CE = 4EA , calculate the ratios
AF : FB .
AP : PD
Markscheme
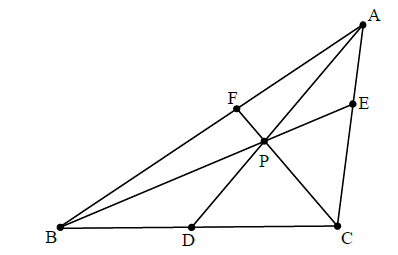
using Ceva's theorem,
\(\frac{{{\rm{BD}}}}{{{\rm{DC}}}} \times \frac{{{\rm{CE}}}}{{{\rm{EA}}}} \times \frac{{{\rm{AF}}}}{{{\rm{FB}}}} = 1\) M1A1
\(\frac{2}{3} \times \frac{4}{1} \times \frac{{{\rm{AF}}}}{{{\rm{FB}}}} = 1\) A1
\(\frac{{{\rm{AF}}}}{{{\rm{FB}}}} = \frac{3}{8}\) or AF : FB \( = 3 : 8\) A1
[4 marks]
using Menelaus' theorem in triangle ACD with BPE as transversal
\(\frac{{{\rm{AE}}}}{{{\rm{EC}}}} \times \frac{{{\rm{CB}}}}{{{\rm{BD}}}} \times \frac{{{\rm{DP}}}}{{{\rm{PA}}}} = - 1\) M1A1
\(\frac{1}{4} \times - \frac{5}{2} \times \frac{{{\rm{DP}}}}{{{\rm{PA}}}} = - 1\) A1
\(\frac{{{\rm{DP}}}}{{{\rm{PA}}}} = \frac{8}{5}\) or AP : PD = 5 : 8 A1
[4 marks]
Examiners report
This proved difficult for many candidates and often the ratios and negative signs were "blurred".
This proved difficult for many candidates and often the ratios and negative signs were "blurred".

