| Date | May 2008 | Marks available | 7 | Reference code | 08M.2.hl.TZ0.3 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 3 | Adapted from | N/A |
Question
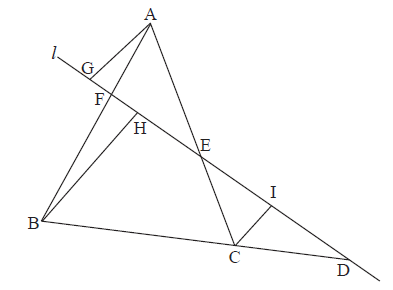
The diagram shows the line l meeting the sides of the triangle ABC at the points D, E and F. The perpendiculars to l from A, B and C meet l at G, H and I.
(i) State why AFFB=AGHB .
(ii) Hence prove Menelaus’ theorem for the triangle ABC.
(iii) State and prove the converse of Menelaus’ theorem.
A straight line meets the sides (PQ), (QR), (RS), (SP) of a quadrilateral PQRS at the points U, V, W, X respectively. Use Menelaus’ theorem to show thatPUUQ×QVVR×RWWS×SXXP=1.
Markscheme
(i) Because the triangles AGF and BHF are similar. R1
(ii) It follows (by cyclic rotation or considering similar triangles) that
BDDC=BHIC A1
and CEEA=CIGA A1
Multiplying these three results gives Menelaus’ Theorem, i.e.
AFFB×BDDC×CEEA=AGHB×BHIC×CIGA M1A1
=AGGA×BHHB×CIIC=−1 M1A1
(iii) The converse states that if D, E, F are points on the sides (BC), (CA), (AB) of a triangle such that
AFFB×BDDC×CEEA=−1
then D, E, F are collinear. A1
To prove this result, let D, E, F′ be collinear points on the three sides so that, using the above theorem, M1
AF′F′B×BDDC×CEEA=−1 A1
Since AFFB×BDDC×CEEA=−1 M1
AF′F′B=AFFB A1
and F=F′ which proves the converse. R1
[13 marks]
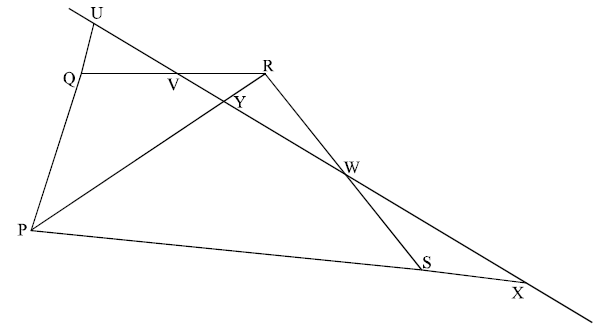
Draw the diagonal PR and let it cut the line at the point Y. M1
Apply Menelaus’ Theorem to the triangle PQR. Then,
PUUQ×QVVR×RYYP=−1 M1A1
Now apply the theorem to triangle PRS.
PYYR×RWWS×SXXP=−1 A1
PUUQ×QVVR×RYYP×PYYR×RWWS×SXXP=−1×−1 M1
⇒PUUQ×QVVR×RWWS×SXXP×PYYP×RYYR=1 A1
⇒PUUQ×QVVR×RWWS×SXXP×(−1)×(−1)=1 (M1)
⇒PUUQ×QVVR×RWWS×SXXP=1 AG
[7 marks]
