| Date | May 2012 | Marks available | 7 | Reference code | 12M.1.hl.TZ0.4 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Show that | Question number | 4 | Adapted from | N/A |
Question
The diagram below shows a quadrilateral ABCD and a straight line which intersects (AB), (BC), (CD), (DA) at the points P, Q, R, S respectively.
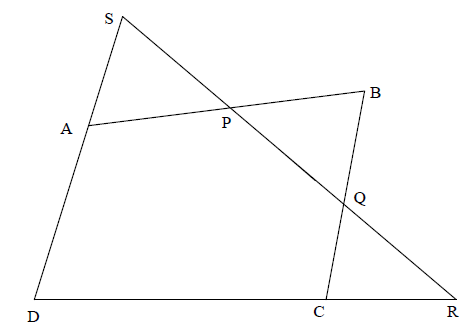
Using Menelaus’ theorem, show that \(\frac{{{\rm{AP}}}}{{{\rm{PB}}}} \times \frac{{{\rm{BQ}}}}{{{\rm{QC}}}} \times \frac{{{\rm{CR}}}}{{{\rm{RD}}}} \times \frac{{{\rm{DS}}}}{{{\rm{SA}}}} = 1\) .
Markscheme
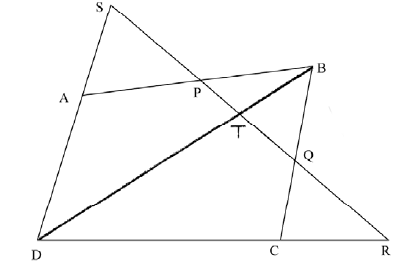
join BD and let the transversal meet (BD) at T (A1)
apply Menelaus’ theorem to triangle ABD with transversal (RS) : M1
\(\frac{{{\rm{AP}}}}{{{\rm{PB}}}} \times \frac{{{\rm{BT}}}}{{{\rm{TD}}}} \times \frac{{{\rm{DS}}}}{{{\rm{SA}}}} = ( - )1\) A1
apply Menelaus’ theorem to triangle CBD with transversal (RS) : M1
\(\frac{{{\rm{AP}}}}{{{\rm{PB}}}} \times \frac{{{\rm{BQ}}}}{{{\rm{QC}}}} \times \frac{{{\rm{CR}}}}{{{\rm{RD}}}} \times \frac{{{\rm{DT}}}}{{{\rm{TB}}}} = ( - )1\) A1
multiplying these two results,
\(\frac{{{\rm{AP}}}}{{{\rm{PB}}}} \times \frac{{{\rm{BT}}}}{{{\rm{TD}}}} \times \frac{{{\rm{DS}}}}{{{\rm{SA}}}} \times \frac{{{\rm{BQ}}}}{{{\rm{QC}}}} \times \frac{{{\rm{CR}}}}{{{\rm{RD}}}} \times \frac{{{\rm{DT}}}}{{{\rm{TB}}}} = 1\) M1A1
whence
\(\frac{{{\rm{AP}}}}{{{\rm{PB}}}} \times \frac{{{\rm{BQ}}}}{{{\rm{QC}}}} \times \frac{{{\rm{CR}}}}{{{\rm{RD}}}} \times \frac{{{\rm{DS}}}}{{{\rm{SA}}}} = 1\) AG
Note: The question can also be solved by joining AC and letting the transversal meet (AC) at T. Menelaus’ Theorem then has to be applied to triangles ABC and ACD.
The relevant equations are \(\frac{{{\rm{AP}}}}{{{\rm{PB}}}} \times \frac{{{\rm{BQ}}}}{{{\rm{QC}}}} \times \frac{{{\rm{CT}}}}{{{\rm{TA}}}} = ( - )1\) and \(\frac{{{\rm{CT}}}}{{{\rm{TA}}}} \times \frac{{{\rm{AS}}}}{{{\rm{SD}}}} \times \frac{{{\rm{DR}}}}{{{\rm{RC}}}} = ( - )1\) .
[7 marks]
Examiners report
Questions on pure geometry which require an initial construction to be made are usually either well done or not done at all and this was no exception. The obvious construction was to draw the line BD and use Menelaus’ Theorem twice although some candidates took the more difficult route by joining AC which also leads to the solution. However, many candidates did not start the question at all or tried to apply Menelaus’ Theorem to existing triangles which was not a successful approach. The examiners saw a number of candidates who produced well set out and well-explained solutions, but there were still a significant number of cases where diagrams were not fully labelled and points were referred to in the working that were not on the diagram. Candidates should realise that to ensure full marks on questions involving geometric proof that there is a certain degree of formality required in the solution.

