| Date | May 2007 | Marks available | 13 | Reference code | 07M.2.hl.TZ0.3 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 3 | Adapted from | N/A |
Question
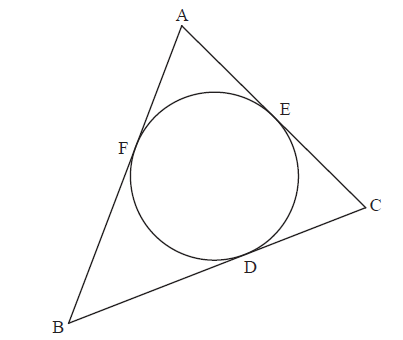
The diagram shows triangle ABC together with its inscribed circle. Show that [AD], [BE] and [CF] are concurrent.
PQRS is a parallelogram and T is a point inside the parallelogram such that the sum of \({\rm{P}}\hat {\rm{T}}{\rm{Q}}\) and \({\rm{R}}\hat {\rm{T}}{\rm{S}}\) is \({180^ \circ }\) . Show that \({\rm{TP}} \times {\rm{TR}} + {\rm{ST}} \times {\rm{TQ}} = {\rm{PQ}} \times {\rm{QR}}\) .
Markscheme
Since the lengths of the two tangents from a point to a circle are equal (M1)
\({\rm{AF = AE, BF = BD, CD = CE}}\) A1
Consider
\(\frac{{{\rm{AF}}}}{{{\rm{FB}}}} \times \frac{{{\rm{BD}}}}{{{\rm{DC}}}} \times \frac{{{\rm{CE}}}}{{{\rm{EA}}}} = 1\) (signed lengths are not relevant here) M2A2
It follows by the converse to Ceva’s Theorem that [AD], [BE], [CF] are concurrent. R2
[8 marks]
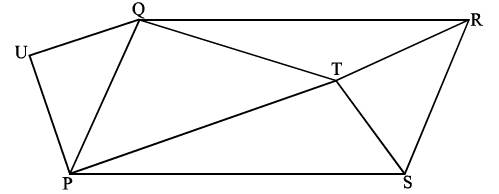
Draw the \(\Delta {\rm{PQU}}\) congruent to \(\Delta {\rm{SRT}}\) (or translate \(\Delta {\rm{SRT}}\) to form \(\Delta {\rm{PQU}}\) ). R2
Since \({\rm{P}}\hat {\rm{U}}{\rm{Q}} = {\rm{S}}\hat {\rm{T}}{\rm{R}}\) , and \({\rm{S}}\hat {\rm{T}}{\rm{R + P}}\hat {\rm{T}}{\rm{Q}} = {180^ \circ }\) it follows that R2
\({\rm{P}}\hat {\rm{U}}{\rm{Q + P}}\hat {\rm{T}}{\rm{Q}} = {180^ \circ }\) R1
The quadrilateral PUQT is therefore cyclic R2
Using Ptolemy’s Theorem, M2
\({\rm{UQ}} \times {\rm{PT}} + {\rm{PU}} \times {\rm{QT}} = {\rm{PQ}} \times {\rm{UT}}\) A2
Since \({\rm{UQ = TR}}\) , \({\rm{PU = ST}}\) and \({\rm{UT = QR}}\) R2
Then \({\rm{TP}} \times {\rm{TR}} + {\rm{ST}} \times {\rm{TQ}} = {\rm{PQ}} \times {\rm{QR}}\) AG
[13 marks]

