| Date | May 2011 | Marks available | 6 | Reference code | 11M.2.hl.TZ0.2 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Prove that | Question number | 2 | Adapted from | N/A |
Question
ABCD is a quadrilateral. (AD) and (BC) intersect at F and (AB) and (CD) intersect at H. (DB) and (CA) intersect (FH) at G and E respectively. This is shown in the diagram below.
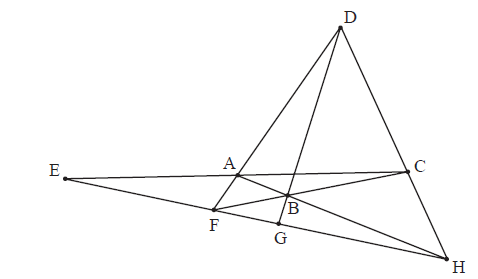
Prove that \(\frac{{{\rm{HG}}}}{{{\rm{GF}}}} = - \frac{{{\rm{HE}}}}{{{\rm{EF}}}}\) .
Markscheme
in \(\Delta {\rm{HFD}}\) , [HA], [FC] and [DG] are concurrent at B M1
so, \(\frac{{{\rm{HG}}}}{{{\rm{GF}}}} \times \frac{{{\rm{FA}}}}{{{\rm{AD}}}} \times \frac{{{\rm{DC}}}}{{{\rm{CH}}}} = 1\) by Ceva’s theorem A1R1
in \(\Delta {\rm{HFD}}\) , with CAE as transversal, M1
\(\frac{{{\rm{HE}}}}{{{\rm{EF}}}} \times \frac{{{\rm{FA}}}}{{{\rm{AD}}}} \times \frac{{{\rm{DC}}}}{{{\rm{CH}}}} = - 1\) by Menelaus’ theorem A1R1
therefore, \(\frac{{{\rm{HG}}}}{{{\rm{GF}}}} = - \frac{{{\rm{HE}}}}{{{\rm{EF}}}}\) AG
[6 marks]
Examiners report
This was not a difficult question but again too many candidates often left gaps in their solutions perhaps thinking that what they were doing was obvious and needed no written support

