| Date | May 2010 | Marks available | 7 | Reference code | 10M.2.hl.TZ0.2 |
| Level | HL only | Paper | 2 | Time zone | TZ0 |
| Command term | Show that | Question number | 2 | Adapted from | N/A |
Question
The points D, E, F lie on the sides [BC], [CA], [AB] of the triangle ABC and [AD], [BE], [CF] intersect at the point G. You are given that CD \( = 2\)BD and AG \( = 2\)GD .
By considering (BE) as a transversal to the triangle ACD, show that
\(\frac{{{\rm{CE}}}}{{{\rm{EA}}}} = \frac{3}{2}\) .
Determine the ratios
(i) \(\frac{{{\rm{AF}}}}{{{\rm{FB}}}}\) ;
(ii) \(\frac{{{\rm{BG}}}}{{{\rm{GE}}}}\) .
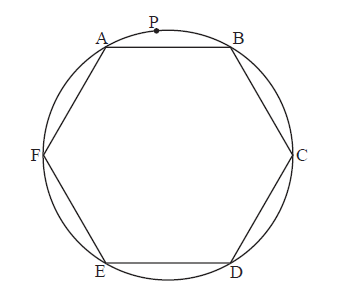
The diagram shows a hexagon ABCDEF inscribed in a circle. All the sides of the hexagon are equal in length. The point P lies on the minor arc AB of the circle. Using Ptolemy’s theorem, show that\[{\rm{PE}} + {\rm{PD}} = {\rm{PA}} + {\rm{PB}} + {\rm{PC}} + {\rm{PF}}\]
Markscheme
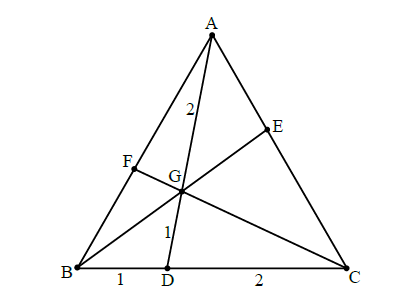
using Menelaus’ theorem in \(\Delta {\rm{ACD}}\) ,
\(\frac{{{\rm{CE}}}}{{{\rm{EA}}}} \bullet \frac{{{\rm{AG}}}}{{{\rm{GD}}}} \bullet \frac{{{\rm{DB}}}}{{{\rm{BC}}}} = - 1\) M1
\(\frac{{{\rm{CE}}}}{{{\rm{EA}}}} \bullet \frac{2}{1} \bullet \frac{1}{3} = 1\) A1
\(\frac{{{\rm{CE}}}}{{{\rm{EA}}}} = \frac{3}{2}\) AG
[2 marks]
(i) using Ceva’s theorem in \(\Delta {\rm{ABC}}\) ,
\(\frac{{{\rm{CE}}}}{{{\rm{EA}}}} \bullet \frac{{{\rm{AF}}}}{{{\rm{FB}}}} \bullet \frac{{{\rm{BD}}}}{{{\rm{DC}}}} = 1\) M1
\(\frac{3}{2} \bullet \frac{{{\rm{AF}}}}{{{\rm{FB}}}} \bullet \frac{1}{2} = 1\) A1
\(\frac{{{\rm{AF}}}}{{{\rm{FB}}}} = \frac{4}{3}\) A1
(ii) using Menelaus’ theorem in \(\Delta {\rm{ABE}}\) , with traversal (FC), M1
\(\frac{{{\rm{AF}}}}{{{\rm{FB}}}} \bullet \frac{{{\rm{BG}}}}{{{\rm{GE}}}} \bullet \frac{{{\rm{EC}}}}{{{\rm{CA}}}} = - 1\) A1
\(\frac{4}{3} \bullet \frac{{{\rm{BG}}}}{{{\rm{GE}}}} \bullet \frac{3}{5} = 1\) A1
\(\frac{{{\rm{BG}}}}{{{\rm{GE}}}} = \frac{5}{4}\) A1
[7 marks]
using Ptolemy’s theorem in PAEC, M1
\({\rm{PA}} \bullet {\rm{EC}} + {\rm{AE}} \bullet {\rm{PC = PE}} \bullet {\rm{AC}}\) A1
since \({\rm{EC = AE = AC}}\) , M1
\({\rm{PE = PA + PC}}\) A1
similarly for PBDF, M1
\({\rm{PB \bullet DF + BD \bullet PF = PD \bullet BF}}\) (A1)
\({\rm{PD = PB + PF}}\) A1
adding these results,
\({\rm{PE + PD = PA + PB + PC + PF}}\) AG
[7 marks]
Examiners report
Part A was reasonably well done by many candidates. It would appear from the scripts that, in general, candidates find Menelaus’ Theorem more difficult to apply than Ceva’s Theorem, probably because the choice of transversal is not always obvious.
Part A was reasonably well done by many candidates. It would appear from the scripts that, in general, candidates find Menelaus’ Theorem more difficult to apply than Ceva’s Theorem, probably because the choice of transversal is not always obvious.
Few fully correct answers were seen to part B with most candidates unable to identify which cyclic quadrilaterals should be used.

