| Date | None Specimen | Marks available | 8 | Reference code | SPNone.1.hl.TZ0.15 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Prove that | Question number | 15 | Adapted from | N/A |
Question
Prove the internal angle bisector theorem, namely that the internal bisector of an angle of a triangle divides the side opposite the angle into segments proportional to the sides adjacent to the angle.
The bisector of the exterior angle \(\widehat A\) of the triangle ABC meets (BC) at P. The bisector of the interior angle \(\widehat B\) meets [AC] at Q. Given that (PQ) meets [AB] at R, use Menelaus’ theorem to prove that (CR) bisects the angle \({\rm{A}}\widehat {\rm{C}}{\rm{B}}\) .
Markscheme
EITHER

let [AD] bisect A, draw a line through C parallel to (AD) meeting (AB) at E M1
then \({\rm{B}}\widehat {\rm{A}}{\rm{D}} = {\rm{A}}\widehat {\rm{E}}{\rm{C}}\) and \({\rm{D}}\widehat {\rm{A}}{\rm{C}} = {\rm{A}}\widehat {\rm{C}}{\rm{E}}\) A1
since \({\rm{B}}\widehat {\rm{A}}{\rm{D}} = {\rm{D}}\widehat {\rm{A}}{\rm{C}}\) it follows that \({\rm{A}}\widehat {\rm{E}}{\rm{C}} = {\rm{A}}\widehat {\rm{C}}{\rm{E}}\) A1
triangle AEC is therefore isosceles and \({\rm{AE}} = {\rm{AC}}\) A1
since triangles BAD and BEC are similar
\(\frac{{{\rm{BD}}}}{{{\rm{DC}}}} = \frac{{{\rm{AB}}}}{{{\rm{AE}}}} = \frac{{{\rm{AB}}}}{{{\rm{AC}}}}\) M1A1
OR
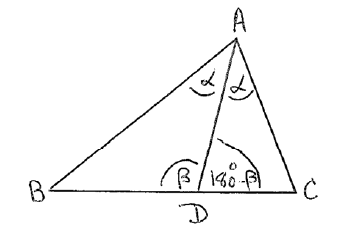
\(\frac{{{\rm{AB}}}}{{\sin \beta }} = \frac{{{\rm{BD}}}}{{\sin \alpha }}\) M1A1
\(\frac{{{\rm{AC}}}}{{\sin (180 - \beta )}} = \frac{{{\rm{DC}}}}{{\sin \alpha }}\) M1A1
\(\sin \beta = \sin (180 - \beta )\) R1
\( \Rightarrow \frac{{{\rm{AB}}}}{{{\rm{BD}}}} = \frac{{{\rm{AC}}}}{{{\rm{DC}}}}\)
\( \Rightarrow \frac{{{\rm{BD}}}}{{{\rm{DC}}}} = \frac{{{\rm{AB}}}}{{{\rm{AC}}}}\) A1
[6 marks]
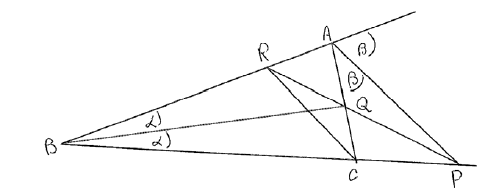
using the angle bisector theorem, M1
\(\frac{{{\rm{AQ}}}}{{{\rm{QC}}}} = \frac{{{\rm{AB}}}}{{{\rm{BC}}}}\) and \(\frac{{{\rm{BP}}}}{{{\rm{PC}}}} = \frac{{{\rm{AB}}}}{{{\rm{BC}}}}\) A1
using Menelaus’ theorem with (PR) as transversal to triangle ABC M1
\(\frac{{{\rm{BR}}}}{{{\rm{AR}}}} \times \frac{{{\rm{AQ}}}}{{{\rm{QC}}}} \times \frac{{{\rm{PC}}}}{{{\rm{BP}}}} = ( - )1\) A1
substituting the above results, M1
\(\frac{{{\rm{BR}}}}{{{\rm{AR}}}} \times \frac{{{\rm{AB}}}}{{{\rm{BC}}}} \times \frac{{{\rm{AC}}}}{{{\rm{AB}}}} = ( - )1\) A1
giving
\(\frac{{{\rm{BR}}}}{{{\rm{AR}}}} = \frac{{{\rm{BC}}}}{{{\rm{AC}}}}\) A1
[CR] therefore bisects angle C by (the converse to) the angle bisector theorem R1AG
[8 marks]

