| Date | May 2017 | Marks available | 2 | Reference code | 17M.1.sl.TZ2.4 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 4 | Adapted from | N/A |
Question
Line \(L\) intersects the \(x\)-axis at point A and the \(y\)-axis at point B, as shown on the diagram.
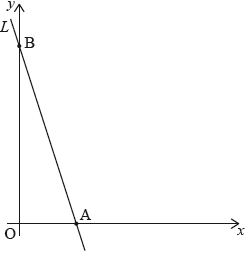
The length of line segment OB is three times the length of line segment OA, where O is the origin.
Point \({\text{(2, 6)}}\) lies on \(L\).
Find the gradient of \(L\).
Find the equation of \(L\) in the form \(y = mx + c\).
Find the \(x\)-coordinate of point A.
Markscheme
\( - 3\) (A1)(A1) (C2)
Notes: Award (A1) for 3 and (A1) for a negative value.
Award (A1)(A0) for either \(3x\) or \( - 3x\).
[2 marks]
\(6 = - 3(2) + c\)\(\,\,\,\)OR\(\,\,\,\)\((y - 6) = - 3(x - 2)\) (M1)
Note: Award (M1) for substitution of their gradient from part (a) into a correct equation with the coordinates \((2,{\text{ }}6)\) correctly substituted.
\(y = - 3x + 12\) (A1)(ft) (C2)
Notes: Award (A1)(ft) for their correct equation. Follow through from part (a).
If no method seen, award (A1)(A0) for \(y = - 3x\).
Award (A1)(A0) for \( - 3x + 12\).
[2 marks]
\(0 = - 3x + 12\) (M1)
Note: Award (M1) for substitution of \(y = 0\) in their equation from part (b).
\((x = ){\text{ }}4\) (A1)(ft) (C2)
Notes: Follow through from their equation from part (b). Do not follow through if no method seen. Do not award the final (A1) if the value of \(x\) is negative or zero.
[2 marks]

