| Date | May 2014 | Marks available | 3 | Reference code | 14M.1.sl.TZ1.9 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Deduce | Question number | 9 | Adapted from | N/A |
Question
The diagram shows the points M(a, 18) and B(24, 10) . The straight line BM intersects the y-axis at A(0, 26). M is the midpoint of the line segment AB.
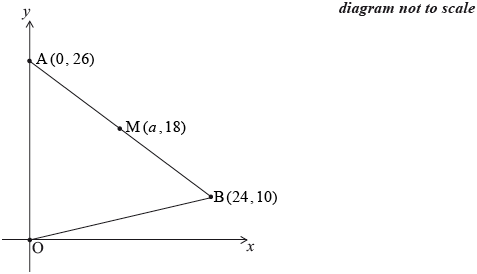
Write down the value of \(a\).
Find the gradient of the line AB.
Decide whether triangle OAM is a right-angled triangle. Justify your answer.
Markscheme
12 (A1) (C1)
Note: Award (A1) for \(\left( {12,18} \right)\).
[1 mark]
\(\frac{{26 - 10}}{{0 - 24}}\) (M1)
Note: Accept \(\frac{{26 - 18}}{{0 - 12}}\) or \(\frac{{18 - 10}}{{12 - 24}}\) (or equivalent).
\( = - \frac{2}{3}{\text{ }}\left( { - \frac{{16}}{{24}},{\text{ }} - 0.666666 \ldots } \right)\) (A1) (C2)
Note: If either of the alternative fractions is used, follow through from their answer to part (a).
The answer is now (A1)(ft).
[2 marks]
gradient of \({\text{OM}} = \frac{3}{2}\) (A1)(ft)
Note: Follow through from their answer to part (b).
\( - \frac{2}{3} \times \frac{3}{2}\) (M1)
Note: Award (M1) for multiplying their gradients.
Since the product is \(-1\), OAM is a right-angled triangle (R1)(ft)
Notes: Award the final (R1) only if their conclusion is consistent with their answer for the product of the gradients.
The statement that OAM is a right-angled triangle without justification is awarded no marks.
OR
\({(26 - 18)^2} + {12^2}\) and \({12^2} + {18^2}\) (A1)(ft)
\(\left( {{{(26 - 18)}^2} + {{12}^2}} \right) + ({12^2} + {18^2}) = {26^2}\) (M1)
Note: This method can also be applied to triangle OMB.
Follow through from (a).
Hence a right angled triangle (R1)(ft)
Note: Award the final (R1) only if their conclusion is consistent with their (M1) mark.
OR
\(OA = OB = 26\) (cm) an isosceles triangle (A1)
Note: Award (A1) for \(OA = 26\) (cm) and \(OB = 26\) (cm).
Line drawn from vertex to midpoint of base is perpendicular to the base (M1)
Conclusion (R1) (C3)
Note: Award, at most (A1)(M0)(R0) for stating that OAB is an isosceles triangle without any calculations.
[3 marks]

