| Date | May 2014 | Marks available | 4 | Reference code | 14M.1.sl.TZ2.7 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Determine | Question number | 7 | Adapted from | N/A |
Question
The diagram shows a wheelchair ramp, \({\text{A}}\), designed to descend from a height of \(80{\text{ cm}}\).
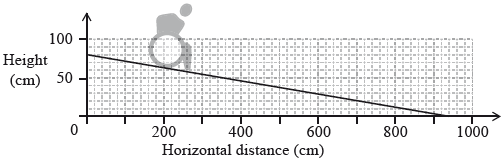
Use the diagram above to calculate the gradient of the ramp.
The gradient for a safe descending wheelchair ramp is \( - \frac{1}{{12}}\).
Using your answer to part (a), comment on why wheelchair ramp \({\text{A}}\) is not safe.
The equation of a second wheelchair ramp, B, is \(2x + 24y - 1920 = 0\).
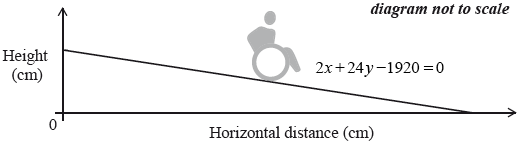
(i) Determine whether wheelchair ramp \({\text{B}}\) is safe or not. Justify your answer.
(ii) Find the horizontal distance of wheelchair ramp \({\text{B}}\).
Markscheme
\( - \frac{{80}}{{940}}{\text{ }}\left( {-0.0851, -0.085106 \ldots , -\frac{4}{{47}}} \right)\) (A1) (C1)
[1 mark]
\(-0.0851{\text{ }} (-0.085106 \ldots ) < - \frac{1}{{12}}(-0.083333 \ldots )\) (A1)(ft) (C1)
Notes: Accept “less than” in place of inequality.
Award (A0) if incorrect inequality seen.
Follow through from part (a).
[1 mark]
(i) ramp \({\text{B}}\) is safe (A1)
the gradient of ramp \({\text{B}}\) is \( - \frac{1}{{12}}\) (R1)
Notes: Award (R1) for “the gradient of ramp \({\text{B}}\) is \( - \frac{1}{{12}}\)” seen.
Do not award (A1)(R0).
(ii) \(2x = 1920\) (M1)
Note: Accept alternative methods.
\(960 {\text{ (cm)}}\) (A1) (C4)
[4 marks]

