| Date | November 2014 | Marks available | 3 | Reference code | 14N.2.sl.TZ0.6 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
The following diagram shows two triangles, OBC and OBA, on a set of axes. Point C lies on the \(y\)-axis, and O is the origin.
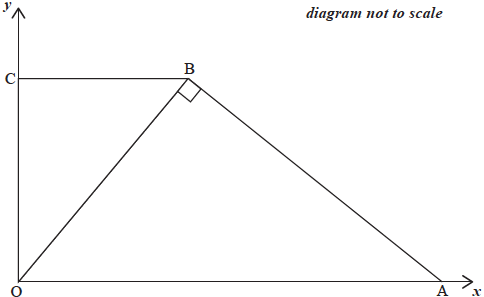
The equation of the line BC is \(y = 4\).
Write down the coordinates of point C.
The \(x\)-coordinate of point B is \(a\).
(i) Write down the coordinates of point B;
(ii) Write down the gradient of the line OB.
Point A lies on the \(x\)-axis and the line AB is perpendicular to line OB.
(i) Write down the gradient of line AB.
(ii) Show that the equation of the line AB is \(4y + ax - {a^2} - 16 = 0\).
The area of triangle AOB is three times the area of triangle OBC.
Find an expression, in terms of a, for
(i) the area of triangle OBC;
(ii) the x-coordinate of point A.
Calculate the value of \(a\).
Markscheme
\((0,{\text{ }}4)\) (A1)
Notes: Accept \(x = 0,{\text{ }}y = 4\).
(i) \((a,{\text{ }}4)\) (A1)(ft)
Notes: Follow through from part (a).
(ii) \(\frac{4}{a}\) (A1)(ft)
Note: Follow through from part (b)(i).
(i) \( - \frac{a}{4}\) (A1)(ft)
Note: Follow through from part (b)(ii).
(ii) \(y = - \frac{a}{4}x + c\) (M1)
Note: Award (M1) for substitution of their gradient from part (c)(i) in the equation.
\(4 = - \frac{a}{4} \times a + c\)
\(c = \frac{1}{4} \times {a^2} + 4\)
\(y = - \frac{a}{4}x + \frac{1}{4}{a^2} + 4\) (A1)
OR
\(y - 4 = - \frac{a}{4}(x - a)\) (M1)
Note: Award (M1) for substitution of their gradient from part (c)(i) in the equation.
\(y = - \frac{{ax}}{4} + \frac{{{a^2}}}{4} + 4\) (A1)
\(4y = - ax + {a^2} + 16\)
\(4y + ax - {a^2} - 16 = 0\) (AG)
Note: Both the simplified and the not simplified equations must be seen for the final (A1) to be awarded.
(i) \(2a\) (A1)
(ii) \(\frac{{4x}}{2} = 3 \times 2a\) (M1)
Note: Award (M1) for correct equation.
\(x = 3a\) (A1)(ft)
Note: Follow through from part (d)(i).
OR
\(0 - 4 = - \frac{a}{4}(x - a)\) (M1)
Note: Award (M1) for correct substitution of their gradient and the coordinates of their point into the equation of a line.
\(\frac{{16}}{a} = x - a\)
\(x = a + \frac{{16}}{a}\) (A1)(ft)
Note: Follow through from parts (b)(i) and (c)(i).
OR
\(4 \times 0 + ax - {a^2} - 16 = 0\) (M1)
Note: Award (M1) for correct substitution of the coordinates of \({\text{A}}(x,{\text{ }}0)\) into the equation of line AB.
\(ax - {a^2} - 16 = 0\)
\(x = a + \frac{{16}}{a}\;\;\;\)OR\(\;\;\;x = \frac{{({a^2} + 16)}}{a}\) (A1)(G1)
\(4(0) + a(3a) - {a^2} - 16 = 0\) (M1)
Note: Award (M1) for correct substitution of their \(3a\) from part (d)(ii) into the equation of line AB.
OR
\(\frac{1}{2}\left( {a + \frac{{16}}{a}} \right) \times 4 = 3\left( {\frac{{4a}}{2}} \right)\) (M1)
Note: Award (M1) for area of triangle AOB (with their substituted \(a + \frac{{16}}{a}\) and 4) equated to three times their area of triangle AOB.
\(a = 2.83\;\;\;\left( {2.82842...,{\text{ }}2\sqrt 2 ,{\text{ }}\sqrt 8 } \right)\) (A1)(ft)(G1)
Note: Follow through from parts (d)(i) and (d)(ii).

