| Date | November 2008 | Marks available | 3 | Reference code | 08N.2.sl.TZ0.6 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 6 | Adapted from | N/A |
Question
A ship leaves port A on a bearing of \(030^\circ \) . It sails a distance of \(25{\text{ km}}\) to point B. At B, the ship changes direction to a bearing of \(100^\circ \) . It sails a distance of \(40{\text{ km}}\) to reach point C. This information is shown in the diagram below.
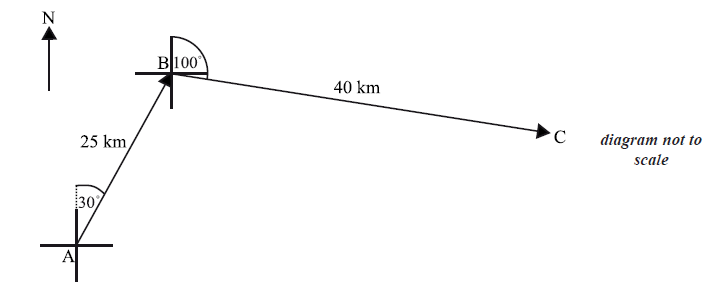
A second ship leaves port A and sails directly to C.
Find the distance the second ship will travel.
Find the bearing of the course taken by the second ship.
Markscheme
finding \({\text{A}}\widehat {\rm{B}}{\rm{C}} = 110^\circ \) (\( = 1.92\) radians) (A1)
evidence of choosing cosine rule (M1)
e.g. \({\rm{A}}{{\rm{C}}^2} = {\rm{A}}{{\rm{B}}^2} + {\rm{B}}{{\rm{C}}^2} - 2({\rm{AB}})({\rm{BC}})\cos {\rm{A}}\widehat {\rm{B}}{\rm{C}}\)
correct substitution A1
e.g. \({\rm{A}}{{\rm{C}}^2} = {25^2} + {40^2} - 2(25)(40)\cos 110^\circ \)
\({\rm{A}}{{\rm{C}}^{}} = 53.9\) (km) A1
METHOD 1
correct substitution into the sine rule A1
e.g. \(\frac{{\sin {\rm{B}}\widehat {\rm{A}}{\rm{C}}}}{{40}} = \frac{{\sin 110^\circ }}{{53.9}}\) A1
\({\rm{B}}\widehat {\rm{A}}{\rm{C}} = 44.2^\circ \)
bearing \( = 074^\circ \) A1 N1
METHOD 2
correct substitution into the cosine rule A1
e.g. \(\cos {\rm{B}}\widehat {\rm{A}}{\rm{C}} = \frac{{{{40}^2} - {{25}^2} - {{53.9}^2}}}{{ - 2(25)(53.9)}}\) A1
\({\rm{B}}\widehat {\rm{A}}{\rm{C}} = 44.3^\circ \)
bearing \( = 074^\circ \) A1 N1
[3 marks]
Examiners report
A good number of candidates found this question very accessible, although some attempted to use Pythagoras' theorem to find AC.
Often candidates correctly found \({\rm{B}}\widehat {\rm{A}}{\rm{C}}\) in part (b), but few added the \(30^\circ \) to obtain the required bearing. Some candidates calculated \({\rm{B}}\widehat {\rm{C}}{\rm{A}}\) , misinterpreting that the question required the course of the second ship.

