| Date | November 2010 | Marks available | 5 | Reference code | 10N.1.sl.TZ0.8 |
| Level | SL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find and Hence | Question number | 8 | Adapted from | N/A |
Question
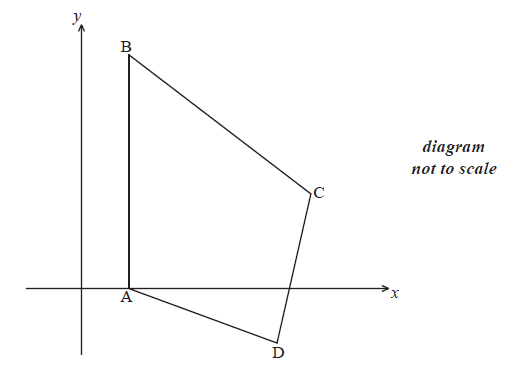
The diagram shows quadrilateral ABCD with vertices A(1, 0), B(1, 5), C(5, 2) and D(4, −1) .
(i) Show that \(\overrightarrow {{\rm{AC}}} = \left( {\begin{array}{*{20}{c}}
4\\
2
\end{array}} \right)\) .
(ii) Find \(\overrightarrow {{\rm{BD}}} \) .
(iii) Show that \(\overrightarrow {{\rm{AC}}} \) is perpendicular to \(\overrightarrow {{\rm{BD}}} \) .
The line (AC) has equation \({\boldsymbol{r}} = {\boldsymbol{u}} + s{\boldsymbol{v}}\) .
(i) Write down vector u and vector v .
(ii) Find a vector equation for the line (BD).
The lines (AC) and (BD) intersect at the point \({\text{P}}(3{\text{, }}k)\) .
Show that \(k = 1\) .
The lines (AC) and (BD) intersect at the point \({\text{P}}(3{\text{, }}k)\) .
Hence find the area of triangle ACD.
Markscheme
(i) correct approach A1
e.g. \(\overrightarrow {{\rm{OC}}} - \overrightarrow {{\rm{OA}}} \) , \(\left( {\begin{array}{*{20}{c}}
5\\
2
\end{array}} \right) - \left( {\begin{array}{*{20}{c}}
1\\
0
\end{array}} \right)\)
\(\overrightarrow {{\rm{AC}}} = \left( {\begin{array}{*{20}{c}}
4\\
2
\end{array}} \right)\) AG N0
(ii) appropriate approach (M1)
e.g. \({\mathop{\rm D}\nolimits} - {\rm{B}}\) , \(\left( {\begin{array}{*{20}{c}}
4\\
{ - 1}
\end{array}} \right) - \left( {\begin{array}{*{20}{c}}
1\\
5
\end{array}} \right)\) , move 3 to the right and 6 down
\(\overrightarrow {{\rm{BD}}} = \left( {\begin{array}{*{20}{c}}
3\\
{ - 6}
\end{array}} \right)\) A1 N2
(iii) finding the scalar product A1
e.g. \(4(3) + 2( - 6)\) , \(12 - 12\)
valid reasoning R1
e.g. \(4(3) + 2( - 6) = 0\) , scalar product is zero
\(\overrightarrow {{\rm{AC}}} \) is perpendicular to \(\overrightarrow {{\rm{BD}}} \) AG N0
[5 marks]
(i) correct “position” vector for u; “direction” vector for v A1A1 N2
e.g. \({\boldsymbol{u}} = \left( {\begin{array}{*{20}{c}}
5\\
2
\end{array}} \right)\) , \({\boldsymbol{u}} = \left( {\begin{array}{*{20}{c}}
1\\
0
\end{array}} \right)\) ; \({\boldsymbol{v}} = \left( {\begin{array}{*{20}{c}}
4\\
2
\end{array}} \right)\) , \({\boldsymbol{v}} = \left( {\begin{array}{*{20}{c}}
{ - 2}\\
{ - 1}
\end{array}} \right)\)
accept in equation e.g. \(\left( {\begin{array}{*{20}{c}}
5\\
2
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
{ - 4}\\
{ - 2}
\end{array}} \right)\)
(ii) any correct equation in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) , where \({\boldsymbol{b}} = \overrightarrow {{\rm{BD}}} \)
\({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
1\\
5
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
3\\
{ - 6}
\end{array}} \right)\) , \(\left( {\begin{array}{*{20}{c}}
x\\
y
\end{array}} \right) = \left( {\begin{array}{*{20}{c}}
4\\
{ - 1}
\end{array}} \right) + t\left( {\begin{array}{*{20}{c}}
{ - 1}\\
2
\end{array}} \right)\) A2 N2
[4 marks]
METHOD 1
substitute (3, k) into equation for (AC) or (BD) (M1)
e.g. \(3 = 1 + 4s\) , \(3 = 1 + 3t\)
value of t or s A1
e.g. \(s = \frac{1}{2}\) , \( - \frac{1}{2}\) , \(t = \frac{2}{3}\) , \( - \frac{1}{3}\)
substituting A1
e.g. \(k = 0 + \frac{1}{2}(2)\)
\(k = 1\) AG N0
METHOD 2
setting up two equations (M1)
e.g. \(1 + 4s = 4 + 3t\) , \(2s = - 1 - 6t\) ; setting vector equations of lines equal
value of t or s A1
e.g. \(s = \frac{1}{2}\) , \( - \frac{1}{2}\) , \(t = \frac{2}{3}\) , \( - \frac{1}{3}\)
substituting A1
e.g. \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
4\\
{ - 1}
\end{array}} \right) - \frac{1}{3}\left( {\begin{array}{*{20}{c}}
3\\
{ - 6}
\end{array}} \right)\)
\(k = 1\) AG N0
[3 marks]
\(\overrightarrow {{\rm{PD}}} = \left( {\begin{array}{*{20}{c}}
1\\
{ - 2}
\end{array}} \right)\) (A1)
\(|\overrightarrow {{\rm{PD}}} | = \sqrt {{2^2} + {1^2}} \) \(( = \sqrt 5 )\) (A1)
\(|\overrightarrow {{\rm{AC}}} | = \sqrt {{4^2} + {2^2}} \) \(( = \sqrt {20} )\) (A1)
area \( = \frac{1}{2} \times |\overrightarrow {{\rm{AC}}} | \times |\overrightarrow {{\rm{PD}}} |\) (\( = \frac{1}{2} \times \sqrt {20} \times \sqrt 5 \)) M1
\( = 5\) A1 N4
[5 marks]
Examiners report
The majority of candidates were successful on part (a), finding vectors between two points and using the scalar product to show two vectors to be perpendicular.
Although a large number of candidates answered part (b) correctly, there were many who had trouble with the vector equation of a line. Most notably, there were those who confused the position vector with the direction vector, and those who wrote their equation in an incorrect form.
In part (c), most candidates seemed to know what was required, though there were many who made algebraic errors when solving for the parameters. A few candidates worked backward, using \(k = 1\) , which is not allowed on a "show that" question.
In part (d), candidates attempted many different geometric and vector methods to find the area of the triangle. As the question said "hence", it was required that candidates should use answers from their previous working - i.e. \({\rm{AC}} \bot {\rm{BD}}\) and \({\text{P}}(3{\text{, }}1)\) . Some geometric approaches, while leading to the correct answer, did not use "hence" or lacked the required justification.

