| Date | May 2012 | Marks available | 7 | Reference code | 12M.2.sl.TZ2.8 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Find | Question number | 8 | Adapted from | N/A |
Question
The following diagram shows the cuboid (rectangular solid) OABCDEFG, where O is the origin, and \(\overrightarrow {{\rm{OA}}} = 4\boldsymbol{i}\) , \(\overrightarrow {{\rm{OC}}} = 3\boldsymbol{j}\) , \(\overrightarrow {{\rm{OD}}} = 2\boldsymbol{k}\) .
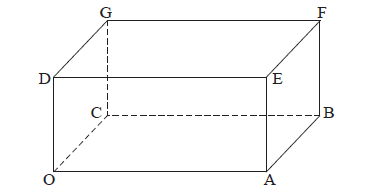
(i) Find \(\overrightarrow {{\rm{OB}}} \) .
(ii) Find \(\overrightarrow {{\rm{OF}}} \) .
(iii) Show that \(\overrightarrow {{\rm{AG}}} = - 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) .
Write down a vector equation for
(i) the line OF;
(ii) the line AG.
Find the obtuse angle between the lines OF and AG.
Markscheme
(i) valid approach (M1)
e.g. \({\rm{OA + OB}}\)
\(\overrightarrow {{\rm{OB}}} = 4{\boldsymbol{i}} + 3{\boldsymbol{j}}\) A1 N2
(ii) valid approach (M1)
e.g. \(\overrightarrow {{\rm{OA}}} {\rm{ + }}\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{BF}}} \) ; \(\overrightarrow {{\rm{OB}}} {\rm{ + }}\overrightarrow {{\rm{BF}}} \) ; \(\overrightarrow {{\rm{OC}}} {\rm{ + }}\overrightarrow {{\rm{CG}}} {\rm{ + }}\overrightarrow {{\rm{GF}}} \)
\(\overrightarrow {{\rm{OF}}} = 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) A1 N2
(iii) correct approach A1
e.g. \(\overrightarrow {{\rm{AO}}} {\rm{ + }}\overrightarrow {{\rm{OC}}} {\rm{ + }}\overrightarrow {{\rm{CG}}} \) ; \(\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{BF}}} {\rm{ + }}\overrightarrow {{\rm{FG}}} \) ; \(\overrightarrow {{\rm{AB}}} {\rm{ + }}\overrightarrow {{\rm{BC}}} {\rm{ + }}\overrightarrow {{\rm{CG}}} \)
\(\overrightarrow {{\rm{AG}}} = - 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) AG N0
[5 marks]
(i) any correct equation for (OF) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + t{\boldsymbol{b}}\) A2 N2
where \({\boldsymbol{a}}\) is 0 or \(4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) , and \({\boldsymbol{b}}\) is a scalar multiple of \(4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\)
e.g. \({\boldsymbol{r}} = t(4{\text{, }}3{\text{, }}2)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{4t}\\
{3t}\\
{2t}
\end{array}} \right)\) , \({\boldsymbol{r}} = 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}} + t(4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}})\)
(ii) any correct equation for (AG) in the form \({\boldsymbol{r}} = {\boldsymbol{a}} + s{\boldsymbol{b}}\) A2 N2
where \({\boldsymbol{a}}\) is \(4{\boldsymbol{i}}\) or \(3{\boldsymbol{j}} + 2{\boldsymbol{k}}\) and \({\boldsymbol{b}}\) is a scalar multiple of \( - 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}}\)
e.g. \({\boldsymbol{r}} = (4{\text{, }}0{\text{, }}0) + s( - 4{\text{, }}3{\text{, }}2)\) , \({\boldsymbol{r}} = \left( {\begin{array}{*{20}{c}}
{4 - 4s}\\
{3s}\\
{2s}
\end{array}} \right)\) , \({\boldsymbol{r}} = 3{\boldsymbol{j}} + 2{\boldsymbol{k}} + s( - 4{\boldsymbol{i}} + 3{\boldsymbol{j}} + 2{\boldsymbol{k}})\)
[4 marks]
choosing correct direction vectors, \(\overrightarrow {{\rm{OF}}} \) and \(\overrightarrow {{\rm{AG}}} \) (A1)(A1)
scalar product \( = - 16 + 9 + 4\) \(( = - 3)\) (A1)
magnitudes \(\sqrt {{4^2} + {3^2} + {2^2}} \) , \(\sqrt {{{( - 4)}^2} + {3^2} + {2^2}} \) , \(\left( {\sqrt {29} ,\sqrt {29} } \right)\) (A1)(A1)
substitution into formula M1
e.g. \(\cos \theta = \frac{{ - 16 + 9 + 4}}{{\left( {\sqrt {{4^2} + {3^2} + {2^2}} } \right) \times \sqrt {{{( - 4)}^2} + {3^2} + {2^2}} }} = \left( { - \frac{3}{{29}}} \right)\)
\(95.93777^\circ \) , \(1.67443{\text{ radians}}\)
\(\theta = 95.9^\circ \) or \(1.67\) A1 N4
[7 marks]
Examiners report
Although a large proportion of candidates managed to answer this question, their biggest challenge was the use of a proper notation to represent the vectors and vector equations of lines.
In part (a), finding \(\overrightarrow {{\rm{OB}}} \) and \(\overrightarrow {{\rm{OF}}} \) was generally well done, although many lost the mark for (iii) due to poor working or not clearly showing the result.
Part (b) was very poorly done. Not all the students recognized which correct position vectors they had to use to write the equations of the lines. It was seen that they frequently failed to present the equations in the required format, which prevented these candidates from achieving full marks. The notations generally seen were \({\text{AG}} = {\boldsymbol{a}} + {\boldsymbol{b}}t\) , \({\boldsymbol{r}} = 4 + t(4{\text{, }}3{\text{, }}2)\) or \(L = {\boldsymbol{a}} + {\boldsymbol{b}}t\) .
Most achieved the correct result in part (c) with many others gaining most of the marks as follow through from choosing incorrect vectors. Some students did not state which vectors had been used, another cause for losing marks. A few showed poor notation, including i, j and k in the working.

