| Date | May 2012 | Marks available | 3 | Reference code | 12M.2.sl.TZ1.10 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Sketch | Question number | 10 | Adapted from | N/A |
Question
The following diagram shows two ships A and B. At noon, ship A was 15 km due north of ship B. Ship A was moving south at 15 km h–1 and ship B was moving east at 11 km h–1.
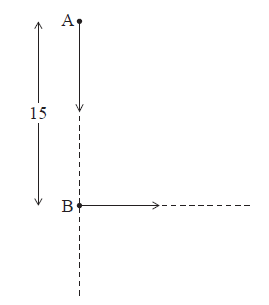
Find the distance between the ships
(i) at 13:00;
(ii) at 14:00.
Let \(s(t)\) be the distance between the ships t hours after noon, for \(0 \le t \le 4\) .
Show that \(s(t) = \sqrt {346{t^2} - 450t + 225} \) .
Sketch the graph of \(s(t)\) .
Due to poor weather, the captain of ship A can only see another ship if they are less than 8 km apart. Explain why the captain cannot see ship B between noon and 16:00.
Markscheme
(i) evidence of valid approach (M1)
e.g. ship A where B was, B \(11{\text{ km}}\) away
\({\text{distance}} = 11\) A1 N2
(ii) evidence of valid approach (M1)
e.g. new diagram, Pythagoras, vectors
\(s = \sqrt {{{15}^2} + {{22}^2}} \) (A1)
\(\sqrt {709} = 26.62705\)
\(s = 26.6\) A1 N2
Note: Award M0A0A0 for using the formula given in part (b).
[5 marks]
evidence of valid approach (M1)
e.g. a table, diagram, formula \(d = r \times t\)
distance ship A travels t hours after noon is \(15(t - 1)\) (A2)
distance ship B travels in t hours after noon is \(11t\) (A1)
evidence of valid approach M1
e.g. \(s(t) = \sqrt {{{\left[ {15(t - 1)} \right]}^2} + {{(11t)}^2}} \)
correct simplification A1
e.g. \(\sqrt {225({t^2} - 2t + 1) + 121{t^2}} \)
\(s(t) = \sqrt {346{t^2} - 450t + 225} \) AG N0
[6 marks]
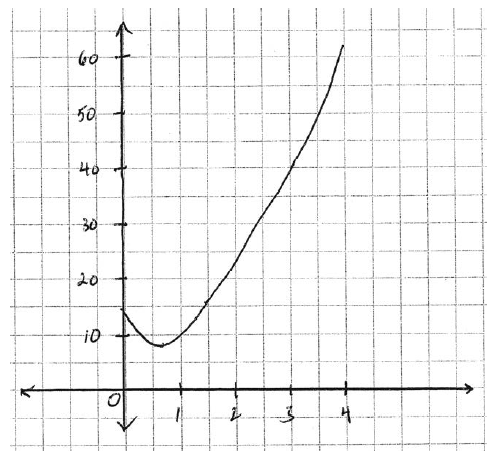 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for shape, A1 for minimum at approximately \((0.7{\text{, }}9)\), A1 for domain.
[3 marks]
evidence of valid approach (M1)
e.g. \(s'(t) = 0\) , find minimum of \(s(t)\) , graph, reference to "more than 8 km"
\(\min = 8.870455 \ldots \) (accept 2 or more sf) A1
since \({s_{\min}} > 8\) , captain cannot see ship B R1 N0
[3 marks]
Examiners report
Part (a) was generally well done although some candidates incorrectly used the function given in part (b) to find the required values. There was evidence that some candidates are not comfortable with a 24-hour clock.
Candidates had difficulty generalizing the problem and therefore, were unable to show how the function \(s(t)\) was obtained in part (b).
Surprisingly, the graph in part (c) was not well done. Candidates often ignored the given domain, provided no indication of scale, and drew "V" shapes or parabolas.
In part (d), candidates simply regurgitated the question without providing any significant evidence for their statements that the two ships must have been more than 8 km apart.

