| Date | November 2012 | Marks available | 3 | Reference code | 12N.2.sl.TZ0.9 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Find | Question number | 9 | Adapted from | N/A |
Question
Consider the function \(f(x) = {x^2} - 4x + 1\) .
Sketch the graph of f , for \( - 1 \le x \le 5\) .
This function can also be written as \(f(x) = {(x - p)^2} - 3\) .
Write down the value of p .
The graph of g is obtained by reflecting the graph of f in the x-axis, followed by a translation of \(\left( {\begin{array}{*{20}{c}}
0\\
6
\end{array}} \right)\) .
Show that \(g(x) = - {x^2} + 4x + 5\) .
The graph of g is obtained by reflecting the graph of f in the x-axis, followed by a translation of \(\left( {\begin{array}{*{20}{c}}
0\\
6
\end{array}} \right)\) .
The graphs of f and g intersect at two points.
Write down the x-coordinates of these two points.
The graph of \(g\) is obtained by reflecting the graph of \(f\) in the x-axis, followed by a translation of \(\left( {\begin{array}{*{20}{c}}
0 \\
6
\end{array}} \right)\) .
Let R be the region enclosed by the graphs of f and g .
Find the area of R .
Markscheme
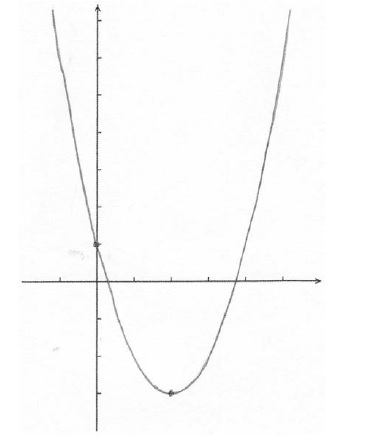 A1A1A1A1 N4
A1A1A1A1 N4
Note: The shape must be an approximately correct upwards parabola.
Only if the shape is approximately correct, award the following:
A1 for vertex \(x \approx 2\) , A1 for x-intercepts between 0 and 1, and 3 and 4, A1 for correct y-intercept \((0{\text{, }}1)\), A1 for correct domain \([ - 1{\text{, }}5]\).
Scale not required on the axes, but approximate positions need to be clear.
[4 marks]
\(p = 2\) A1 N1
[1 mark]
correct vertical reflection, correct vertical translation (A1)(A1)
e.g. \( - f(x)\) , \( - ({(x - 2)^2} - 3)\) , \( - y\) , \( - f(x) + 6\) , \(y + 6\)
transformations in correct order (A1)
e.g. \( - ({x^2} - 4x + 1) + 6\) , \( - ({(x - 2)^2} - 3) + 6\)
simplification which clearly leads to given answer A1
e.g. \( - {x^2} + 4x - 1 + 6\) , \( - ({x^2} - 4x + 4 - 3) + 6\)
\(g(x) = - {x^2} + 4x + 5\) AG N0
Note: If working shown, award A1A1A0A0 if transformations correct, but done in reverse order, e.g. \( - ({x^2} - 4x + 1 + 6)\).
[4 marks]
valid approach (M1)
e.g. sketch, \(f = g\)
\( - 0.449489 \ldots \) , \(4.449489 \ldots \)
\((2 \pm \sqrt 6 )\) (exact), \( - 0.449{\text{ }}[ - 0.450{\text{, }} - 0.449]\) ; \(4.45{\text{ }}[4.44{\text{, }}4.45]\) A1A1 N3
[3 marks]
attempt to substitute limits or functions into area formula (accept absence of \({\rm{d}}x\) ) (M1)
e.g. \(\int_a^b {(( - {x^2}} + 4x + 5) - ({x^2} - 4x + 1)){\rm{d}}x\) , \(\int_{4.45}^{ - 0.449} {(f - g)} \) , \(\int {( - 2{x^2}} + 8x + 4){\rm{d}}x\)
approach involving subtraction of integrals/areas (accept absence of \({\rm{d}}x\) ) (M1)
e.g. \(\int_a^b {( - {x^2}} + 4x + 5) - \int_a^b {({x^2}} - 4x + 1)\) , \(\int {(f - g){\rm{d}}x} \)
\({\rm{area}} = 39.19183 \ldots \)
\({\rm{area}} = 39.2\) \([39.1{\text{, }}39.2]\) A1 N3
[3 marks]
Examiners report
A good number of students provided a clear sketch of the quadratic function within the given domain. Some lost marks as they did not clearly indicate the approximate positions of the most important points of the parabola either by labelling or providing a suitable scale.
There were few difficulties in part (b).
In part (c), candidates often used an insufficient number of steps to show the required result or had difficulty setting out their work logically.
Part (d) was generally done well though many candidates gave at least one answer to fewer than three significant figures, potentially resulting in more lost marks.
In part (e), many candidates were unable to connect the points of intersection found in part (d) with the limits of integration. Mistakes were also made here either using a GDC incorrectly or not subtracting the correct functions. Other candidates tried to divide the region into four areas and made obvious errors in the process. Very few candidates subtracted \(f(x)\) from \(g(x)\) to get a simple function before integrating and there were numerous, fruitless analytical attempts to find the required integral.

