| Date | November 2012 | Marks available | 4 | Reference code | 12N.2.sl.TZ0.7 |
| Level | SL only | Paper | 2 | Time zone | TZ0 |
| Command term | Sketch | Question number | 7 | Adapted from | N/A |
Question
A particle’s displacement, in metres, is given by \(s(t) = 2t\cos t\) , for \(0 \le t \le 6\) , where t is the time in seconds.
On the grid below, sketch the graph of \(s\) .
Find the maximum velocity of the particle.
Markscheme
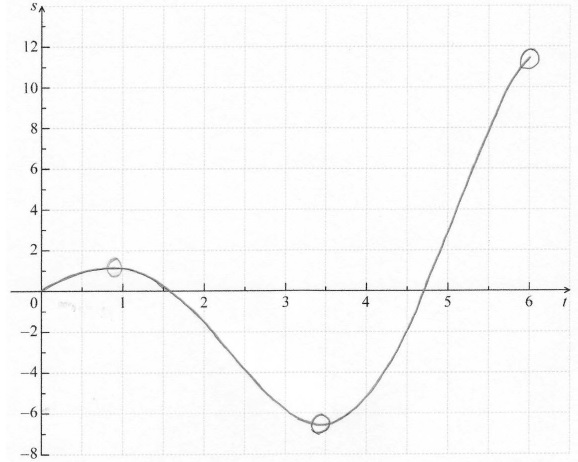 A1A1A1A1 N4
A1A1A1A1 N4
Note: Award A1 for approximately correct shape (do not accept line segments).
Only if this A1 is awarded, award the following:
A1 for maximum and minimum within circles,
A1 for x-intercepts between 1 and 2 and between 4 and 5,
A1 for left endpoint at \((0{\text{, }}0)\) and right endpoint within circle.
[4 marks]
appropriate approach (M1)
e.g. recognizing that \(v = s'\) , finding derivative, \(a = s''\)
valid method to find maximum (M1)
e.g. sketch of \(v\) , \(v'(t) = 0\) , \(t = 5.08698 \ldots \)
\(v = 10.20025 \ldots \)
\(v = 10.2\) \([10.2{\text{, }}10.3]\) A1 N2
[3 marks]
Examiners report
Most candidates sketched an approximately correct shape for the displacement of a particle in the given domain, but many lost marks for carelessness in graphing the local extrema or the right endpoint.
In part (b), most candidates knew to differentiate displacement to find velocity, but few knew how to then find the maximum. Occasionally, a candidate would give the time value of the maximum. Others attempted to incorrectly set the first derivative equal to zero and solve analytically rather than take the maximum value from the graph of the velocity function.

