| Date | May 2012 | Marks available | 4 | Reference code | 12M.2.sl.TZ2.2 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Sketch | Question number | 2 | Adapted from | N/A |
Question
Let \(f(x) = \cos ({{\rm{e}}^x})\) , for \( - 2 \le x \le 2\) .
Find \(f'(x)\) .
On the grid below, sketch the graph of \(f'(x)\) .
Markscheme
\(f'(x) = - {{\rm{e}}^x}\sin ({{\rm{e}}^x})\) A1A1 N2
[2 marks]
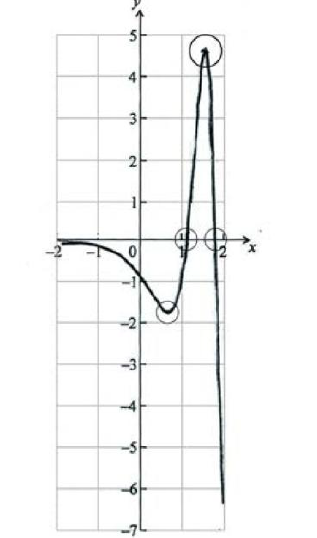A1A1A1A1 N4
Note: Award A1 for shape that must have the correct domain (from \( - 2\) to \( + 2\) ) and correct range (from \( - 6\) to \(4\) ), A1 for minimum in circle, A1 for maximum in circle and A1 for intercepts in circles.
[4 marks]
Examiners report
Many students failed in applying the chain rule to find the correct derivative, and some inappropriately used the product rule. However, many of those obtained full follow through marks in part (b) for the sketch of the function they found in part (a).
Many students failed in applying the chain rule to find the correct derivative, and some inappropriately used the product rule. However, many of those obtained full follow through marks in part (b) for the sketch of the function they found in part (a).
Most candidates sketched an approximately correct shape in the given domain, though there were some that did not realize they had to set their GDC to radians, producing a meaningless sketch.
It is very important to stress to students that although they are asked to produce a sketch, it is still necessary to show its key features such as domain and range, stationary points and intercepts.
