| Date | May 2012 | Marks available | 5 | Reference code | 12M.1.sl.TZ1.9 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Sketch and Write down | Question number | 9 | Adapted from | N/A |
Question
Let \(f(x) = {\log _p}(x + 3)\) for \(x > - 3\) . Part of the graph of f is shown below.
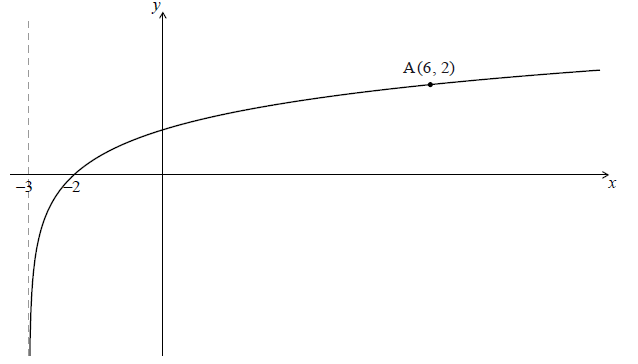
The graph passes through A(6, 2) , has an x-intercept at (−2, 0) and has an asymptote at \(x = - 3\) .
Find p .
The graph of f is reflected in the line \(y = x\) to give the graph of g .
(i) Write down the y-intercept of the graph of g .
(ii) Sketch the graph of g , noting clearly any asymptotes and the image of A.
The graph of \(f\) is reflected in the line \(y = x\) to give the graph of \(g\) .
Find \(g(x)\) .
Markscheme
evidence of substituting the point A (M1)
e.g. \(2 = {\log _p}(6 + 3)\)
manipulating logs A1
e.g. \({p^2} = 9\)
\(p = 3\) A2 N2
[4 marks]
(i) \(y = - 2\) (accept \((0{\text{, }} - 2))\) A1 N1
(ii)
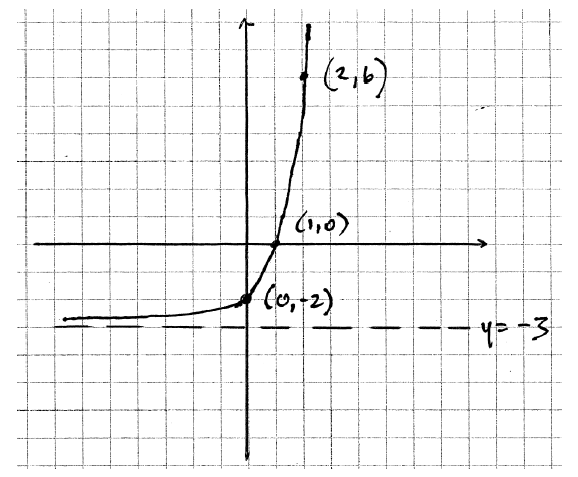A1A1A1A1 N4
Note: Award A1 for asymptote at \(y = - 3\) , A1 for an increasing function that is concave up, A1 for a positive x-intercept and a negative y-intercept, A1 for passing through the point \((2{\text{, }}6)\) .
[5 marks]
METHOD 1
recognizing that \(g = {f^{ - 1}}\) (R1)
evidence of valid approach (M1)
e.g. switching x and y (seen anywhere), solving for x
correct manipulation (A1)
e.g. \({3^x} = y + 3\)
\(g(x) = {3^x} - 3\) A1 N3
METHOD 2
recognizing that \(g(x) = {a^x} + b\) (R1)
identifying vertical translation (A1)
e.g. graph shifted down 3 units, \(f(x) - 3\)
evidence of valid approach (M1)
e.g. substituting point to identify the base
\(g(x) = {3^x} - 3\) A1 N3
[4 marks]
Examiners report
In part (a), many candidates successfully substituted the point A to find the base of the logarithm, although some candidates lost a mark for not showing their manipulation of the logarithm equation into the exponential equation.
A number of candidates who correctly stated the y-intercept was \( - 2\) had difficulty sketching the graph of the reflection in the line \(y = x\) . A number of candidates graphed directly on the question paper rather than sketching their own graph; candidates should be reminded to show all working for Section B on separate paper. Some correct sketches did not have the position of A indicated. Many candidates had difficulty reflecting the asymptote.
Part (c) was often well done, with candidates showing clear and correct working.
The most successful candidates clearly appreciated the linkage between the question parts.
