| Date | May 2012 | Marks available | 3 | Reference code | 12M.2.sl.TZ1.4 |
| Level | SL only | Paper | 2 | Time zone | TZ1 |
| Command term | Write down | Question number | 4 | Adapted from | N/A |
Question
The graph of \(y = (x - 1)\sin x\) , for \(0 \le x \le \frac{{5\pi }}{2}\) , is shown below.
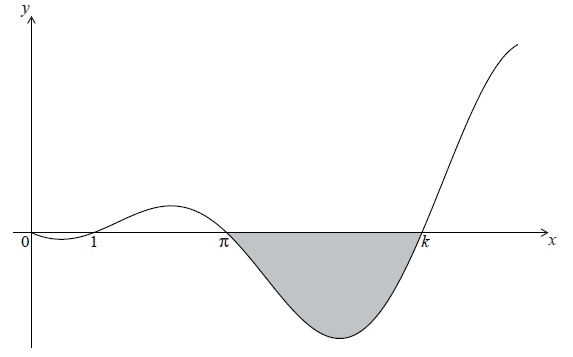
The graph has \(x\)-intercepts at \(0\), \(1\), \( \pi\) and \(k\) .
Find k .
The shaded region is rotated \(360^\circ \) about the x-axis. Let V be the volume of the solid formed.
Write down an expression for V .
The shaded region is rotated \(360^\circ \) about the x-axis. Let V be the volume of the solid formed.
Find V .
Markscheme
evidence of valid approach (M1)
e.g. \(y = 0\) , \(\sin x = 0\)
\(2\pi = 6.283185 \ldots \)
\(k = 6.28\) A1 N2
[2 marks]
attempt to substitute either limits or the function into formula (M1)
(accept absence of \({\rm{d}}x\) )
e.g. \(V = \pi \int_\pi ^k {{{(f(x))}^2}{\rm{d}}x} \) , \(\pi \int {{{((x - 1)\sin x)}^2}} \) , \(\pi \int_\pi ^{6.28 \ldots } {{y^2}{\rm{d}}x} \)
correct expression A2 N3
e.g. \(\pi \int_\pi ^{6.28} {{{(x - 1)}^2}{{\sin }^2}x{\rm{d}}x} \) , \(\pi \int_\pi ^{2\pi } {{{((x - 1)\sin x)}^2}{\rm{d}}x} \)
[3 marks]
\(V = 69.60192562 \ldots \)
\(V = 69.6\) A2 N2
[2 marks]
Examiners report
Candidates showed marked improvement in writing fully correct expressions for a volume of revolution. Common errors of course included the omission of dx , using the given domain as the upper and lower bounds of integration, forgetting to square their function and/or the omission of \(\pi \) . There were still many who were unable to use their calculator successfully to find the required volume.
Candidates showed marked improvement in writing fully correct expressions for a volume of revolution. Common errors of course included the omission of dx , using the given domain as the upper and lower bounds of integration, forgetting to square their function and/or the omission of \(\pi \) . There were still many who were unable to use their calculator successfully to find the required volume.
Candidates showed marked improvement in writing fully correct expressions for a volume of revolution. Common errors of course included the omission of dx, using the given domain as the upper and lower bounds of integration, forgetting to square their function and/or the omission of \(\pi \) . There were still many who were unable to use their calculator successfully to find the required volume.

