| Date | May 2014 | Marks available | 1 | Reference code | 14M.2.sl.TZ2.4 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Shade | Question number | 4 | Adapted from | N/A |
Question
Let \(A\) and \(B\) be independent events, where \({\text{P}}(A) = 0.3\) and \({\text{P}}(B) = 0.6\).
Find \({\text{P}}(A \cap B)\).
[2]
a.
Find \({\text{P}}(A \cup B)\).
[2]
b.
On the following Venn diagram, shade the region that represents \(A \cap B'\).
[1]
c(i).
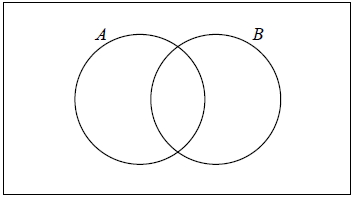
Find \({\text{P}}(A \cap B')\).
[2]
c(ii).
Markscheme
correct substitution (A1)
eg \(0.3 \times 0.6\)
\({\text{P}}(A \cap B) = 0.18\) A1 N2
[2 marks]
a.
correct substitution (A1)
eg \({\text{P}}(A \cup B) = 0.3 + 0.6 - 0.18\)
\({\text{P}}(A \cup B) = 0.72\) A1 N2
[2 marks]
b.
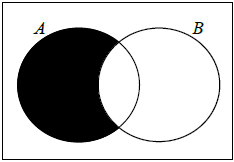A1 N1
c(i).
appropriate approach (M1)
eg \(0.3 - 0.18,{\text{ P}}(A) \times {\text{P}}(B')\)
\({\text{P}}(A \cap B') = 0.12\) (may be seen in Venn diagram) A1 N2
[2 marks]
c(ii).
Examiners report
[N/A]
a.
[N/A]
b.
[N/A]
c(i).
[N/A]
c(ii).
Syllabus sections
Topic 5 - Statistics and probability » 5.5 » Use of Venn diagrams, tree diagrams and tables of outcomes.
Show 32 related questions
