| Date | May 2015 | Marks available | 2 | Reference code | 15M.1.sl.TZ1.10 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
Ann and Bob play a game where they each have an eight-sided die. Ann’s die has three green faces and five red faces; Bob’s die has four green faces and four red faces. They take turns rolling their own die and note what colour faces up. The first player to roll green wins. Ann rolls first. Part of a tree diagram of the game is shown below.
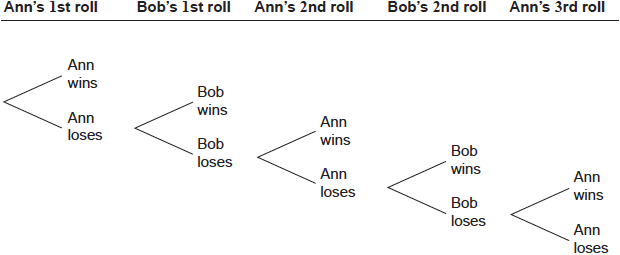
Find the probability that Ann wins on her first roll.
(i) The probability that Ann wins on her third roll is \(\frac{5}{8} \times \frac{4}{8} \times p \times q\ \times \frac{3}{8}\).
Write down the value of \(p\) and of \(q\).
(ii) The probability that Ann wins on her tenth roll is \(\frac{3}{8}{r^k}\) where \(r \in \mathbb{Q},{\text{ }}k \in \mathbb{Z}\).
Find the value of \(r\) and of \(k\).
Find the probability that Ann wins the game.
Markscheme
recognizing Ann rolls green (M1)
eg\(\;\;\;{\text{P(G)}}\)
\(\frac{3}{8}\) A1 N2
[2 marks]
(i) \(p = \frac{4}{8},{\text{ }}q = \frac{5}{8}\) or \(q = \frac{4}{8},{\text{ }}p = \frac{5}{8}\) A1A1 N2
(ii) recognizes Ann and Bob lose \(9\) times (M1)
eg\(\;\;\;\(\overbrace {{A_L}{B_\(\overbrace {{A_L}{B_ \ldots \(\overbrace {{A_L}{B_{\text{ 9 times, }}\underbrace {\left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \ldots \times \left( {\frac{5}{8} \times \frac{4}{8}} \right)}_{{\text{9 times}}}\)
\(k = 9\;\;\;\)(seen anywhere) A1 N2
correct working (A1)
eg\(\;\;\;{\left( {\frac{5}{8} \times \frac{4}{8}} \right)^9} \times \frac{3}{8},{\text{ }}\left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \ldots \times \left( {\frac{5}{8} \times \frac{4}{8}} \right) \times \frac{3}{8}\)
\(r = \frac{{20}}{{64}}\;\;\;\left( { = \frac{5}{{16}}} \right)\) A1 N2
[6 marks]
recognize the probability is an infinite sum (M1)
eg\(\;\;\;\)Ann wins on her \({{\text{1}}^{{\text{st}}}}\) roll or \({{\text{2}}^{{\text{nd}}}}\) roll or \({{\text{3}}^{{\text{rd}}}}\) roll…, \({S_\infty }\)
recognizing GP (M1)
\({u_1} = \frac{3}{8}\;\;\;\)(seen anywhere) A1
\(r = \frac{{20}}{{64}}\;\;\;\)(seen anywhere) A1
correct substitution into infinite sum of GP A1
eg\(\;\;\;\frac{{\frac{3}{8}}}{{1 - \frac{5}{{16}}}},{\text{ }}\frac{3}{8}\left( {\frac{1}{{1 - \left( {\frac{5}{8} \times \frac{4}{8}} \right)}}} \right),{\text{ }}\frac{1}{{1 - \frac{5}{{16}}}}\)
correct working (A1)
eg\(\;\;\;\frac{{\frac{3}{8}}}{{\frac{{11}}{{16}}}},{\text{ }}\frac{3}{8} \times \frac{{16}}{{11}}\)
\({\text{P (Ann wins)}} = \frac{{48}}{{88}}\;\;\;\left( { = \frac{6}{{11}}} \right)\) A1 N1
[7 marks]
Total [15 marks]
Examiners report
Some teachers’ comments suggested that the word ‘loses’ in the diagram was misleading. But candidate scripts did not indicate any adverse effect.
a) Very well answered.
b) i) Probabilities \(p\) and \(q\) were typically found correctly. ii) Fewer candidates identified the common ratio and number of rolls correctly.
Few candidates recognized that this was an infinite geometric sum although some did see that a geometric progression was involved.
Some teachers’ comments suggested that the word ‘loses’ in the diagram was misleading, But candidate scripts did not indicate any adverse effect.
a) Very well answered.
b) i) Probabilities \(p\) and \(q\) were typically found correctly. ii) Fewer candidates identified the common ratio and number of rolls correctly.
Few candidates recognized that this was an infinite geometric sum although some did see that a geometric progression was involved.
Some teachers’ comments suggested that the word ‘loses’ in the diagram was misleading, But candidate scripts did not indicate any adverse effect.
a) Very well answered.
b) i) Probabilities \(p\) and \(q\) were typically found correctly. ii) Fewer candidates identified the common ratio and number of rolls correctly.
Few candidates recognized that this was an infinite geometric sum although some did see that a geometric progression was involved.

