| Date | May 2014 | Marks available | 3 | Reference code | 14M.1.sl.TZ1.9 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Copy and complete | Question number | 9 | Adapted from | N/A |
Question
Bill and Andrea play two games of tennis. The probability that Bill wins the first game is \(\frac{4}{5}\).
If Bill wins the first game, the probability that he wins the second game is \(\frac{5}{6}\).
If Bill loses the first game, the probability that he wins the second game is \(\frac{2}{3}\).
Copy and complete the following tree diagram. (Do not write on this page.)
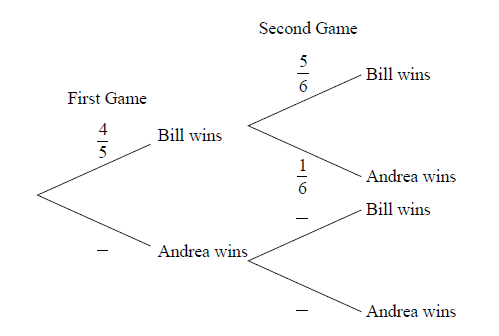
Find the probability that Bill wins the first game and Andrea wins the second game.
Find the probability that Bill wins at least one game.
Given that Bill wins at least one game, find the probability that he wins both games.
Markscheme
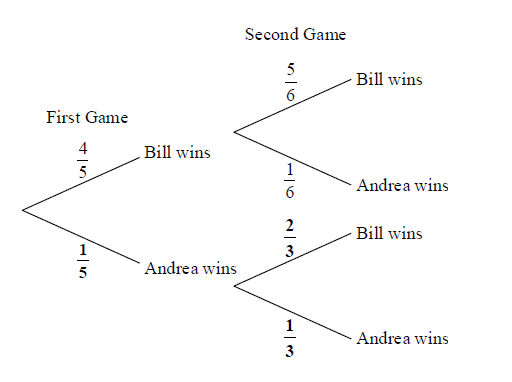 A1A1A1 N3
A1A1A1 N3
Note: Award A1 for each correct bold probability.
[3 marks]
multiplying along the branches (may be seen on diagram) (M1)
eg \(\frac{4}{5} \times \frac{1}{6}\)
\(\frac{4}{{30}}\left( {\frac{2}{{15}}} \right)\) A1 N2
[2 marks]
METHOD 1
multiplying along the branches (may be seen on diagram) (M1)
eg \(\frac{4}{5} \times \frac{5}{6},{\text{ }}\frac{4}{5} \times \frac{1}{6},{\text{ }}\frac{1}{5} \times \frac{2}{3}\)
adding their probabilities of three mutually exclusive paths (M1)
eg \(\frac{4}{5} \times \frac{5}{6} + \frac{4}{5} \times \frac{1}{6} + \frac{1}{5} \times \frac{2}{3},{\text{ }}\frac{4}{5} + \frac{1}{5} \times \frac{2}{3}\)
correct simplification (A1)
eg \(\frac{{20}}{{30}} + \frac{4}{{30}} + \frac{2}{{15}},{\text{ }}\frac{2}{3} + \frac{2}{{15}} + \frac{2}{{15}}\)
\(\frac{{28}}{{30}}{\text{ }}\left( { = \frac{{14}}{{15}}} \right)\) A1 N3
METHOD 2
recognizing “Bill wins at least one” is complement of “Andrea wins 2” (R1)
eg finding P (Andrea wins 2)
P (Andrea wins both) \( = \frac{1}{5} \times \frac{1}{3}\) (A1)
evidence of complement (M1)
eg \(1 - p,{\text{ }}1 - \frac{1}{{15}}\)
\(\frac{{14}}{{15}}\) A1 N3
[4 marks]
P (B wins both) \(\frac{4}{5} \times \frac{5}{6}{\text{ }}\left( { = \frac{2}{3}} \right)\) A1
evidence of recognizing conditional probability (R1)
eg \({\text{P}}(A\left| B \right.),{\text{ P (Bill wins both}}\left| {{\text{Bill wins at least one), tree diagram}}} \right.\)
correct substitution (A2)
eg \(\frac{{\frac{4}{5} \times \frac{5}{6}}}{{\frac{{14}}{{15}}}}\)
\(\frac{{20}}{{28}}{\text{ }}\left( { = \frac{5}{7}} \right)\) A1 N3
[5 marks]

