| Date | May 2011 | Marks available | 2 | Reference code | 11M.1.sl.TZ2.2 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Find | Question number | 2 | Adapted from | N/A |
Question
The Venn diagram below shows events A and B where \({\rm{P}}(A) = 0.3\) , \({\rm{P}}(A \cup B) = 0.6\) and \({\rm{P}}(A \cap B) = 0.1\) . The values m , n , p and q are probabilities.
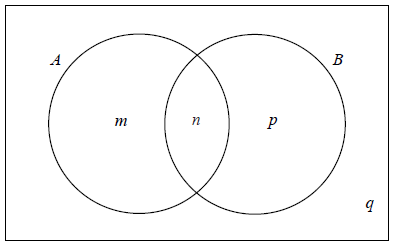
(i) Write down the value of n .
(ii) Find the value of m , of p , and of q .
Find \({\rm{P}}(B')\) .
Markscheme
(i) \(n = 0.1\) A1 N1
(ii) \(m = 0.2\) , \(p = 0.3\) , \(q = 0.4\) A1A1A1 N3
[4 marks]
appropriate approach
e.g. \({\rm{P}}(B') = 1 - P(B)\) , \(m + q\) , \(1 - (n + p)\) (M1)
\({\rm{P}}(B') = 0.6\) A1 N2
[2 marks]
Examiners report
Most candidates were able to find the correct values for the Venn diagram. Unfortunately, however, there were many candidates who did not understand what each region of the diagram represents. For example, a very common error was thinking that \({\rm{P}}(B) = p\) , rather than the correct \({\rm{P}}(B) = p + n\) .
Candidates seemed to understand the idea of the complement in part (b), but some were not able to find the correct answer because of confusion over the separation of the different regions in the diagram.

