| Date | May 2016 | Marks available | 3 | Reference code | 16M.2.sl.TZ2.3 |
| Level | SL only | Paper | 2 | Time zone | TZ2 |
| Command term | Sketch | Question number | 3 | Adapted from | N/A |
Question
Let \(f(x) = {{\text{e}}^{0.5x}} - 2\).
For the graph of f:
(i) write down the \(y\)-intercept;
(ii) find the \(x\)-intercept;
(iii) write down the equation of the horizontal asymptote.
On the following grid, sketch the graph of \(f\), for \( - 4 \leqslant x \leqslant 4\).
Markscheme
(i) \(y = - 1\) A1 N1
(ii) valid attempt to find \(x\)-intercept (M1)
eg\(\,\,\,\,\,\)\(f(x) = 0\)
1.38629 A1 N2
\(x = 2\ln 2{\text{ (exact), }}1.39\)
(iii) \(y = - 2\) (must be equation) A1 N1
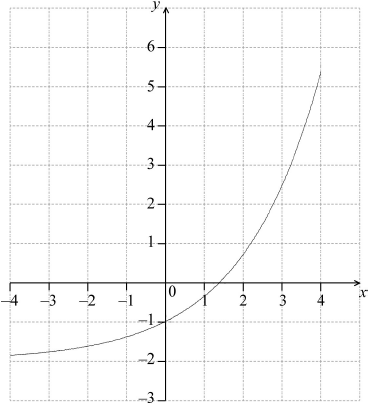 A1A1A1 N3
A1A1A1 N3
[3 marks]
Examiners report
In part a), most candidates were successful at finding the intercepts with the x and y axis, though many failed to write the horizontal asymptote as an equation. Some candidates gave the answer for the horizontal asymptote as \(y \ne - 2\).
For part b), a considerable number of candidates could sketch the exponential function providing an approximately correct shape, although many of them did not use the correct domain, making it go beyond \(x = 4\). Others plotted an incorrect value of \(y\) at \(x = 4\), resulting in the loss of a mark.
Considering that all the question requires from students is to copy the graph off the GDC, it is important to stress which are the features that cannot be missed.

