This is an original paper for you to try. It's equivalent to a Higher Level Paper 2:
- 90 marks
- 5 minutes reading time
- 2 hours 15 minutes
- Print it off and have a go
- Use of a calculator and data booklet are permitted
- Then check out our complete walk-through below
WARNING: Do not attempt this paper until the revision phase of your course. Make the most of the opportunity.
Are you finished?

Are you really finished?

Ok! We'll walk you through it.
Question 1
The centripetal force is the resultant force acting towards the centre that makes a body travel in a circle:
\(F=m \omega^2 r={mv^2 \over r}\)
Vectors are usually drawn with an arrow in the correct direction, where the length of arrow represents the magnitude. A force is an example of a vector.
If the force vectors acting on a body add up to zero then we say they are balanced. To determine if this is the case, resolve the forces into two perpendicular directions (e.g. vertically and horizontally) and see if they cancel out in each.
A trigonometric identity is an equation that applies for any value of angle. The identity that you must learn is: \(\tan \theta={\sin \theta\over \cos\theta}\)
Kinetic energy (Ek) is due to movement, equal to the amount of work required to make a body move.
\(E_k={1\over 2} mv^2\)
Potential energy (Ep) is positional, equal to the amount of work done in taking a body from a place of zero potential energy to the place in question.
\(E_p=mgh\)
When bodies stick together, Ek isn't conserved. Energy is lost. However, momentum is conserved.
Question 2
The ideal gas equation relates pressure, temperature, volume and the amount of gas:
\(pV=nRT\)
To calculate the internal energy, U, of a gas we assume that potential energy is zero:
\(U=\sum E_p+\sum E_k=\sum E_k\)
\(\Rightarrow U=N{3\over 2} kT\)
Boyle's law: The pressure of a fixed mass of gas at constant temperature is inversely proportional to its volume.
\(p\propto{1\over V}\)
Pressure - at a surface and due to movement of particles
Pressure is the ratio of force acting to the surface area. The pressure of the hot gas is greater than the cold because the molecules hit the walls harder and more often due to their increased kinetic energy.
Question 3
Standing waves (or stationary waves) form when the following occurs:
- Two waves
- With the same freqency and amplitude
- Travelling in opposite directions
- Interfere with each other
The most regular occurence of this is a single wave reflecting back onto itself.
Node: Point that has zero amplitude
Wavelength (λ): The distance between two equivalent points on consecutive waves (e.g. peak to peak)
\(v=f\lambda\)
Critical angle: When light travels from glass to air, it refracts away from the normal. If the angle of incidence is large enough then the angle of refraction will be 90°. The angle at which this happens is called the critical angle.
NB: Sound not light. The angle of refraction can be calculated by Snell's law, where n is the refractive index (ratio of the speed of light to its speed in the material).
\({\sin i \over \sin r}={n_2 \over n_1}={v_1\over v_2}\)
Question 4
Potential divider: Any circuit that splits the terminal potential difference of the battery using two or more resistors.
Electromotive force or EMF (ε): The amount of work done per unit charge taking a small positive charge from one side of the battery to the other, when no current is being drawn.
Kirchhoff's second law: The sum of EMF around a closed loop = the sum of the potential difference
\(\sum \varepsilon = \sum V\)
This is a consequence of conservation of energy.
Resistance (R): The ratio of the potential difference across an electrical conductor to the current flowing through it
\(R={V\over I}\)
Resistance is measured in Ohms (Ω).
Question 5
Volume will always be calculated by multiplying three lengths, sometimes with a numerical factor. This means it always has the unit m3.
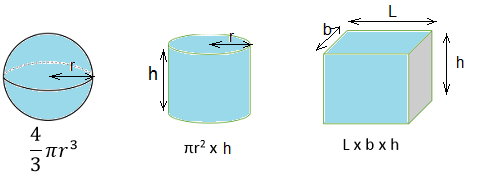
Density is defined as the ratio of the mass of a body to its volume:
\(\rho={m\over V}\)
Potential energy (Ep) is positional, equal to the amount of work done in taking a body from a place of zero potential energy to the place in question.
\(E_p=mgh\)
Power is defined as the rate at which work is done. It is a scalar quantity.
\(P={W\over t}\)
Question 6
The Rutherford model of the atom had the following key ideas:
- A small, densely positive nucleus
- Surrounded by negative electrons
- Neutral overall

Beta particles consist of an electron. Electrons are not normally found in the nucleus, but are released during the process of beta decay, when when a neutron changes into a proton plus an electron. This reduces the ratio of neutrons to protons.
Binding energy is the amount of energy required to pull a nucleus apart into separate nucleons. It is equal to the energy released when the separate nucleons combine to form the overall nucleus.
Beta decay example: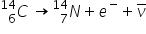

The \(\bar{\nu}\) symbol represents an anti-electron neutrino. The beta energy spectrum provides evidence of the neutrino, which takes some of the kinetic energy:
- Mass - almost nothing
- Charge - zero
- Spin - \(1\over 2\)
The Bohr model predicts the energy of an electron in an energy level as being discrete:
\(E=-{13.6\over n^2}\)
- \(E\) is the energy associated with the \(n^{th}\) energy level (eV)
- \(n\) is the number of the energy level
Angular momentum is also quantised:
\(mvr={nh\over 2\pi}\)
- \(mvr\) is angular momentum (kgm2s-2)
- \(n\) is an integer equal to 1 minus the quantum number
- \(h\) is Planck's constant (Js)
Circular motion and electric forces
The centripetal force is the resultant force acting towards the centre that makes a body travel in a circle.
\(F=m \omega^2 r={mv^2 \over r}\)
The force experienced by two point charges is directly proportional to the product of their charges and inversely proportional to their separation squared:
\(F_E \propto {{q_1 q_2}\over r^2}\)
The proportional sign can be replaced with an equals sign by multiplying by a constant:
\(F_E=k{{q_1 q_2}\over r^2}\)
k is known as Coulomb's constant or the electric force constant. Its value is 8.99×109 N m2 C−2.
Heisenberg's uncertainty principle
The Heisenberg uncertainty principle describes the inherent impossibility of measuring both momentum and position with certainty as an equation:
\(\Delta p \Delta x \geq{h\over 4\pi}\)
- \(\Delta p\) is uncertainty in momentum (kgms-1)
- \(\Delta x\) is uncertainty in position (m)
- \(h\) is Planck's constant (Js)
Question 7
A capacitor contains a uniform electric field. The value of the capacitance of a capacitor is set according to three variables:
\(C=\varepsilon{A\over d}\)
- \(C\) is capacitance (F)
- \(\varepsilon\) is an electric constant (Fm−1)
- \(A\) is the area of overlap of the two plates (m2)
- \(d\) is the separation between the plates (m)
The electric constant is the product of the permittivity of free space and the relative permittivity of the dielectric:
\(\varepsilon=\varepsilon_0k\)
- \(\varepsilon_0\) is the permittivity of space (8.854 x 10-12 Fm-1)
- \(k\) is the permittivity of the dielectric (~1 for air and >1 for all media)
The energy stored when a capacitor is charged can be calculated by adding the infinitesimal stages of work done when each new quantity of charge is added. This is equal to the area under the graph. Since charge stored is proportional to the potential difference across the capacitor:
\(E={1\over 2}qV\)
\(\Rightarrow E={1\over 2}CV^2\)
- \(E\) is the energy stored on the capacitor or the work done that was required to store the charges (J)
Expressions for the variation of charge, current and potential difference with time can be derived:
\(q=q_0e^{-t\over \tau}\)
\(I=I_0e^{-t\over \tau}\)
\(V=V_0e^{-t\over \tau}\)
These equations are exponential decay relationships and have the following characteristic shape when plotted against time:
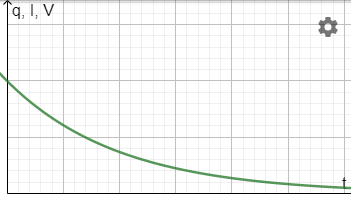
Time constant also has a real-world meaning. It is the product of the capacitance and load resistance (for the circuit diagram shown above):
\(\tau=RC\)
- \(\tau\) is time constant (s)
- \(R\) is load resistance (\(\Omega\))
- \(C\) is capacitance (F)
Resistivity (ρ): The resistance of a material with cross-sectional area of 1 m2 and length 1 m.
\(\rho ={RA\over l}\)
Resistivity has the unit Ωm (which you can work out from the dimensions of the equation).
Question 8
We can determine the position of the first minimum using the approximation equation:
\(\theta = {\lambda \over a}\)
- \(\theta\) is the angle subtended at the slit by the first minimum and the centre (rad)
- \(\lambda\) is the wavelength of the light (m)
- \(a\) is the width of the slit (m)

Since the angle is small, we can also state that it is approximately equal to the ratio of the distance to the minimum and the distance from the slit to the screen:
\(\theta = {y\over D}\)
- \(y\) is the distance between the centre and the first minimum (on either side since symmetrical) (m)
- \(D\) is the distance from the slit to the screen (m)
The phenonoma discussed rely on coherent light. Coherent light beams have constant phase difference (and therefore the same frequency). They should also have the same amplitude.
The fringe spacing can be calculated as follows:
\(s={D\lambda\over d}\)
- \(s\) is the distance between consecutive maxima (m)
- \(D\) is the distance from the slits to the screen (m)
- \(\lambda\) is the wavelength of light (m)
- \(d\) is the distance separating the centres of the two slits (m)
The result is a pattern of evenly spaced bright fringes separated by dark fringes. It is caused by the interference of the light from the two slits as the two paths to each point on the screen vary in distance. The central maximum is most intense.
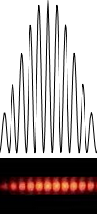

The two-slit interference pattern is modulated by the one-slit diffraction effect.
This affects the distribution of intensity against distance on the screen from the centre by capping the double slit pattern within the intensity of the diffraction pattern.
Brightness: directly related to the intensity (power per unit area), brightness is proportional to the square of the amplitude.
Question 9
Every particle of mass attracts every other particle with a force that is directly proportional to the product of their masses and inversely proportional to their separation squared.
\(F=G{Mm \over r^2}\)
In this equation, \(G\) is the universal gravitational constant, 6.67 × 10-11 m3kg-1s-2.
Forces are said to be balanced if the resultant force is zero. The body is then in equilibrium.
Equal forces are balanced only if they act in opposite directions.
Circular motion and vertical circles
The centripetal force is the resultant force acting towards the centre that makes a body travel in a circle.
\(F=m \omega^2 r={mv^2 \over r}\)
In a 'cyclist on an igloo' problem, the rider is travelling in a vertical circle but on the outside.
The centripetal force is therefore: \(mg-N={mv^2\over r}\)
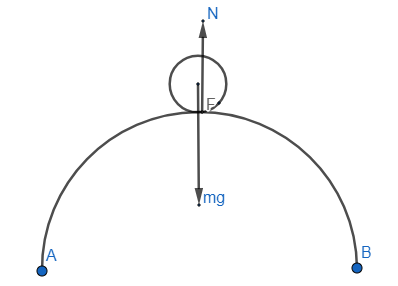
Friction is a force that opposes the motion of a body in contact with a surface.
Friction acts parallel to and along the contact surface. However, it is proportional to the normal force between the surfaces:
\(F=\mu N\)
The constant of proportionality, \(\mu\) = the coefficient of friction, and varies depending on whether the body is stationary (static friction, \(\mu_s\)) or moving (dynamic friction, \(\mu_d\)).
Energy transfers in a radial gravitational field
Kinetic energy (Ek) is due to movement, equal to the amount of work required to make a body move.
\(E_k={1\over 2} mv^2\)
When a mass moves parallel to a field line, its potential energy changes. Potential energy is the product of potential and the mass placed in the field:
\(E_p=mV_g=-G{Mm\over r}\)
Change in potential energy can be calculated as follows:
\(\Delta E_p=m\Delta V_g=m\times GM({1\over r_f}-{1\over r_i})\)
A mass in orbit in a gravitational field possesses two types of energy:
- Kinetic energy due to its motion, \(E_k={1\over 2}mv^2\)
- Gravitational potential energy due to its position in the field, \(E_p=-G{Mm\over r}\)
Total energy, \(E_T=E_k+E_p\):
\(E_T={1\over 2}mv^2-G{Mm\over r}\)
The escape speed is the speed that would just be enough to escape the field.
\(E_k+E_p=0\)
\(\Rightarrow v_\text{esc}=\sqrt{2G{M\over r}}\)
By now you will have a feel for the number of marks you have obtained overall. It's worth being a bit conservative when coming up with a grade, but here is a rough guide:
- 0-10 marks: 1
- 11-20 marks: 2
- 21-30 marks: 3
- 31-40 marks: 4
- 41-50 marks: 5
- 51-60 marks: 6
- 61-90 marks: 7
Feedback
Which of the following best describes your feedback?


 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn