 Nuclear physics is a big topic, embracing all of the following:
Nuclear physics is a big topic, embracing all of the following:
- The nucleus - protons and neutrons, mass unit and nuclear radius
- Fundamental forces - including the strong nuclear force
- Nuclear radiation - types of particle and their properties
- Nuclear decay - calculating how the number of nuclei change over time
- Strong nuclear force - binding energy and mass defect
- Fission and fusion - processes and stability
Key Concepts
Protons and neutrons
All nuclei are made of nucleons, two types of particle: protons and neutrons. They have almost the same mass.
- Protons have a positive charge (and is the same as the hydrogen nucleus)
- Neutrons have no charge
On the Periodic table and in nuclear equations, we use symbols to represent the numbers of protons and neutrons in nuclear reactions:
A is the nucleon number = protons + neutrons (approximately equal to the mass)
Z is the atomic number = protons (Ze equals the charge in Coulombs)
N is the neutron number = neutrons (A - Z)
A typical atomic symbol on the periodic table (for element 'C'): 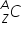
Elements are defined by the number of protons. All atoms of a given element therefore have the same Z but can have different N. This dictates the chemical properties of a given element due to the particular nuclear charge.
Isotopes of an element have the same number of protons but different number of neutrons. Isotopes have the same chemical properties but different physical properties (e.g boiling point).
A neutral atom has the same number of electrons as protons. If the number is different the atom will have a net charge. A charged particle is called an ion.
Unified mass unit (u)
Since the mass of nuclei is based on multiples of protons and neutrons, which themselves have masses in the order of 10-27 kg, it is sensible to define a unit for the nuclear scale: unified mass unit.

1u = 1.66054 x 10-27 kg
This gives the following masses for our nucleons:
| Proton | 1.00728 u |
| Neutron | 1.00866 u |
Nuclear radius
Nuclei are too small for us to observe. However, we can get an approximation by finding the closest distance of a approach when a positive alpha particle is fired at a nucleus.


When particles of matter meet the equivalent particles of antimatter, they annihilate. This led Einstein to his famous mass-energy formula.
\(E=mc^2\)
c = the speed of light in a vacuum (3 x 108 ms-1)
The signficance of this equation is that we can calculate the amount of energy required to be converted into the mass of a particle, and vice versa.
How much of Nuclear physics have you understood?


 The physics course to date has taught us about two fundamental forces:
The physics course to date has taught us about two fundamental forces:

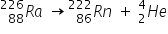
 From this spectrum we can deduce that there are two alpha energies: one at 5.5 MeV and the other at about 5.45 MeV.
From this spectrum we can deduce that there are two alpha energies: one at 5.5 MeV and the other at about 5.45 MeV.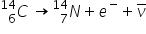
 The
The  Note that both alpha and beta radiation produce new elements.
Note that both alpha and beta radiation produce new elements.  Half life is a constant for a given isotope, and a mathematical outcome of exponential decay.
Half life is a constant for a given isotope, and a mathematical outcome of exponential decay.

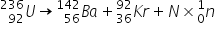

 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn