 Pythagoras' Theorem relates the lengths of the sides of a right-angled triangle.
Pythagoras' Theorem relates the lengths of the sides of a right-angled triangle.
Trigonometry is the manipulation of the lengths and angles of all triangles.
Key Concepts
The sum of the squares of the two shorter sides equals the square of the hypotenuse (longest side).
\(a^2+b^2=c^2\)

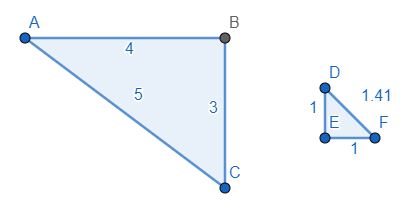
- A triangle of short sides 3 and 4 will have a long side length 5.
- An isosceles triangle of short sides 1 and 1 will have a long side length \(\sqrt2 \) (incidentally an irrational number!).
Pythagoras' Theorem also applies in 3-dimensions.

We note that triangle ABD has a right angle at B (since AB is vertical and AD is horizontal). To find the length of side BD we use Pythagoras: \(BD^2=BC^2 +CD^2\)
Length AD can then be obtained using substitution: \(AD^2=AB^2+BD^2 = AB^2+BC^2+CD^2 \)
How much of Pythagoras and trigonometry have you understood?


 In IB Physics you are only required to perform trigonometry for right angled triangles.
In IB Physics you are only required to perform trigonometry for right angled triangles.


 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn