Because there are no gravitational or electrostatic forces between gas molecules (elastic Collisions), the gaseous state is the simplest to model.
In this section of the course, we will be linking the microscopic concept of kinetic energy of individual molecules with the macroscopic concepts of pressure, temperature and volume.
Key Concepts
The absolute temperature of a gas (in Kelvin) is directly proportional to the average kinetic energy of the molecules.
\(\bar{E_k}={3\over2} kT\)
k is the Boltzmann constant 1.38 x 10-23 JK-1
Pressure = force \(\div\) area. The force exerted by the gas molecules is due to their change of momentum as they hit the walls (due to Newton's second law).
Boyle's law: The pressure of a fixed mass of gas at constant temperature is inversely proportional to its volume.
\(p\propto{1\over V}\)
To verify that a gas obeys Boyle's Law, you can measure the pressure of gas in a syringe as the volume is reduced. This must be done slowly to keep the temperature constant. Alternatively, your school may have 'gas syringes' connected to pressure sensors.
If p is proportional to 1/V then a graph of p vs V will be a curve.
Note that this particular curve is for higher pressures and temperatures than would be found in the classroom!
The curve is called an isothermal as it's at constant temperature. To verify the relationship, you would need to plot p against \(1\over V\)to yield a straight line through the origin (Linear graphs).
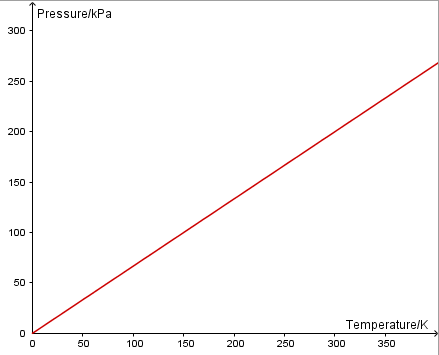
Pressure Law: The pressure of a fixed mass of gas with constant volume is directly proportional to its absolute temperature (in Kelvin).
\(p\propto T\)
A pressure sensor is used to measure the pressure of a fixed volume of gas as its temperature is changed. Software will then enable you to plot p vs T.
Since pressure is directly proportional to absolute temperature, a graph of p vs T will be linear and through the origin.
Charles' Law: The volume of a fixed mass of gas at a constant pressure is directly proportional to its temperature in Kelvin.
\(V \propto T\)
To verify Charles' law, measure the volume of a fixed mass of gas at different temperatures. This needs a piston that moves very smoothly; ask if your school Physics department has the PASCO apparatus.
The temperature of the air in the metal can is changed by placing it in a water bath. As the water is heated, the gas expands pushing the piston up.
Since volume is proportional to temperature, a graph of V vs T will be linear and through the origin.
The three laws can be combined to produce a single equation. As well as pressure, volume and temperature, the ideal gas equation also includes the number of moles of the gas, n, and a constant of proportionality, R.
\(pV=nRT\)
- \(n\) is the number of moles
- \(R\) is the molar gas constant = 8.31 Jmol-1K-1
This is represented by a p-V graph. Different temperatures are represented by different isothermals.
Much like contours for height on a map, the isothermals are plotted at constant intervals (every 500 K).
Deviations from the ideal gas model
Recall that we made several assumptions about the particles of a gas:
- very small, relative to the size of the container
- perfectly elastic collisions
- time between collisions >> time of a collision
- spherical
- identical
- have no forces between them unless colliding
Which of these assumptions would not be true for a real gas at high pressure?
How much of Modelling gases have you understood?
Twitter 
Facebook 
LinkedIn