On this page you can find examination questions from the topic of calculus


Find the value(s) of x for which the graph \(y=x^3-8x+2\) has gradient 4
Hint
Full Solution
Print from here


Find \(f'(4)\) for the function \(f(x)=2x+\frac { 8 }{ \sqrt { x } } +\frac { 32 }{ x } \)
Hint
Full Solution
Print from here


The gradient of \(y=x^2+ax+b\) at the point (1,-3) is -4.
Find a and b
Hint
x=1 when y = -3
\(\frac{dy}{dx}=-4\) when x = 1
Full Solution
Print from here


The graph of y = f(x) is shown below, where B is a local maximum and C is a local minimum
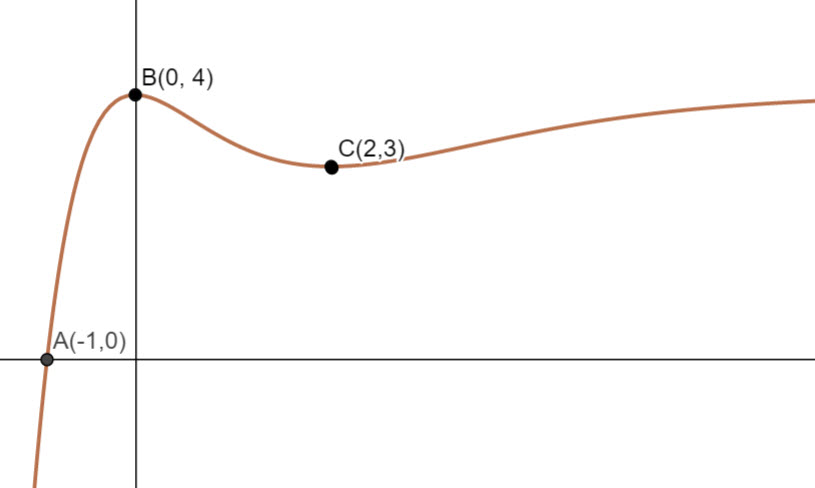
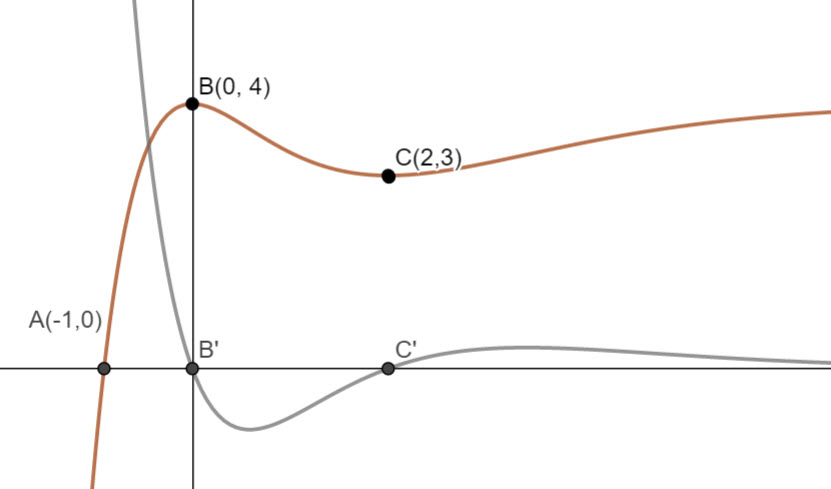
Sketch a graph of y = f'(x), clearly showing the images of the points B and C labellling them B' and C' respectively
Hint
B and C are a stationary points - gradient = 0
Full Solution


A function is given by \(f(x)=-x^3+6x^2+4\)
a) Find the coordinates of any stationary points and describe their nature
b) Determine the values of x such that f(x) is a increasing function
c) Find the coordinates of the point of inflexion
Hint
a) Solve f'(x)=0
c) point of inflexion is non-stationary solve f''(x)=0
Full Solution
Print from here


The following diagram shows the graph of \(f'\), the derivative of f
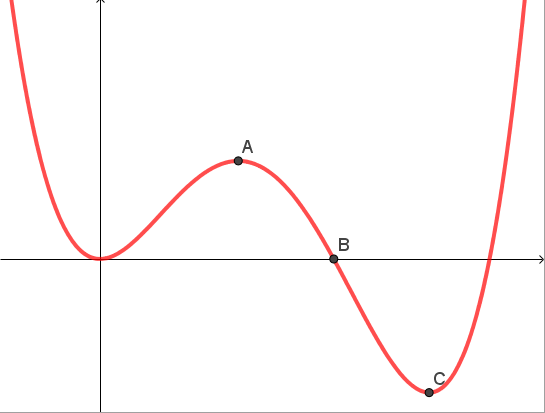
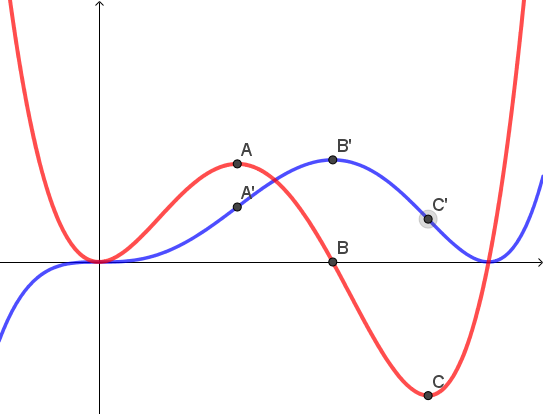
On the graph below, sketch the graph of y = f(x) given that f(0) = 0. Mark the images of A , B and C labelling them A' , B' and C'.

Hint
Consider where the gradient function is zero -> stationary points.
The gradient of f' is zero, what does this mean?
Full Solution


Consider the function \(f(x)=-x^3-3x^2+9x\)
a) Find the coordinates of any stationary points and determine their nature
b) Find the equation of the straight line that passes through both the local maximum and the local minimum points.
c) Show that the point of inflexion lies on this line.
Hint
a) Stationary points occur when f'(x)=0
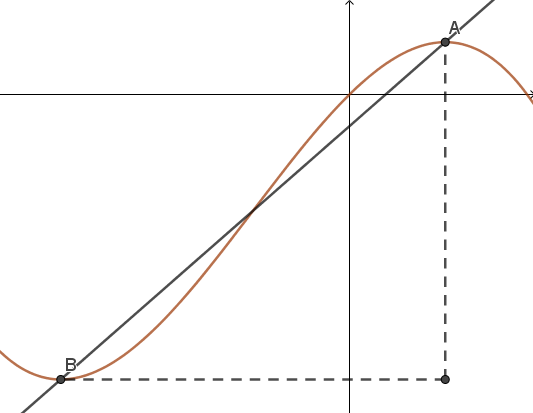
c) Point of inflexion must be non-stationary. Solve \(f''(x)=0\)
Full Solution
Print from here


Let \(y=xe^x\)
a) Find \(\frac{dy}{dx}\)
b) Show that \(\frac{d^2y}{dx^2}=e^x(2+x)\)
c) Find the coordinates of the stationary point and show that it is a local minimum.
Hint
a) Use the Product Rule to find \(\frac{dy}{dx}\)
c) Solve \(\frac{dy}{dx}=0\) to find position of stationary point. Show that \(\frac{d^2y}{dx^2}>0\)
Full Solution
Print from here


Let \(f(x)={ x }^{ 2 }{ (2x-3) }^{ 3 }\)
a) Find \(f'(x)\)
b) The graph of y = f(x) has stationary points at x = 0, x= \(\frac{3}{2}\) and x = a. Find the value of a
Hint
a) You need to use the chain rule to differentiate \({ (2x-3) }^{ 3 }\)
Full Solution
Print from here


Let \(f(x)=\frac{lnx}{x},x>0\)
a) Show that \(f'(x)=\frac{1-lnx}{x^2}\)
b) Find \(f''(x)\)
c) The graph of f has a point of inflexion at A. Find the x-coordinate of A.
Hint
a) Use the Quotient Rule to find \(f'(x)\)
c) Solve \(f''(x)=0\) to find point of inflexion
Full Solution
Print from here


Let \(f(x)=tanx\). A\((\frac{\pi}{3},\sqrt{3})\) is a point that lies on the graph of \(y=f(x)\)
a) Given that \(tanx=\frac{sinx}{cosx}\) find \(f'(x)\)
b) Show that \(f'(\frac{\pi}{3})=4\)
c) Find the equation of the normal to the curve y = f(x) at the point A
d) Show that the normal crosses the y axis at \(\sqrt{3}+\frac{\pi}{12}\)
Hint
a) Use the quotient rule to differentiate tanx
Full Solution
Print from here

Let \(f(x)=e^{2x}cosx\)
a) Find \(f'(x)\)
b) Show that \(f''(x)=4f'(x)-5f(x)\)
Hint
a) Use the Product Rule to find \(f'(x)\)
b) Use Product Rule again to find \(f''(x)\)
Full Solution
Print from here


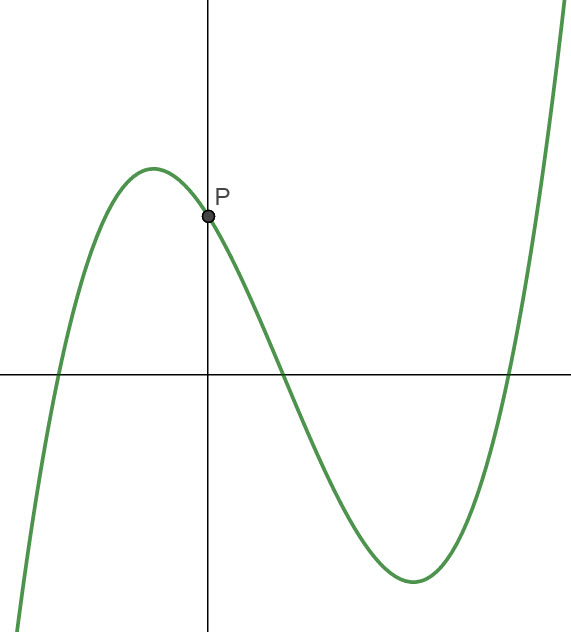
Let f(x) = (x - 1)(x - 4)(x + 2). The diagram below shows the graph of f and the point P where the graph crosses the x axis.
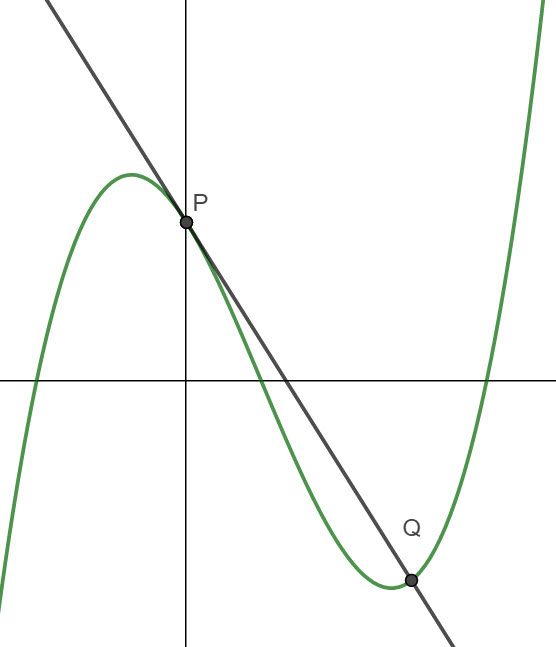
The line L is the tangent to the graph of f at the point P.
The line L intersects the graph of f at another point Q, as shown below
a) Find the coordinates of P
b) Show that \(f(x)=x^3-3x^2-6x+8\)
c) Find the equation of L in the form y = ax + b
d) Find the x coordinate of Q.
Hint
b) Expand the brackets carefully. For example, you could expand (x - 4)(x + 2) first. Once done multiple (x - 1) by your result.
d) Solve \(−6x+8=x^3−3x^2−6x+8\)
Full Solution
Print from here


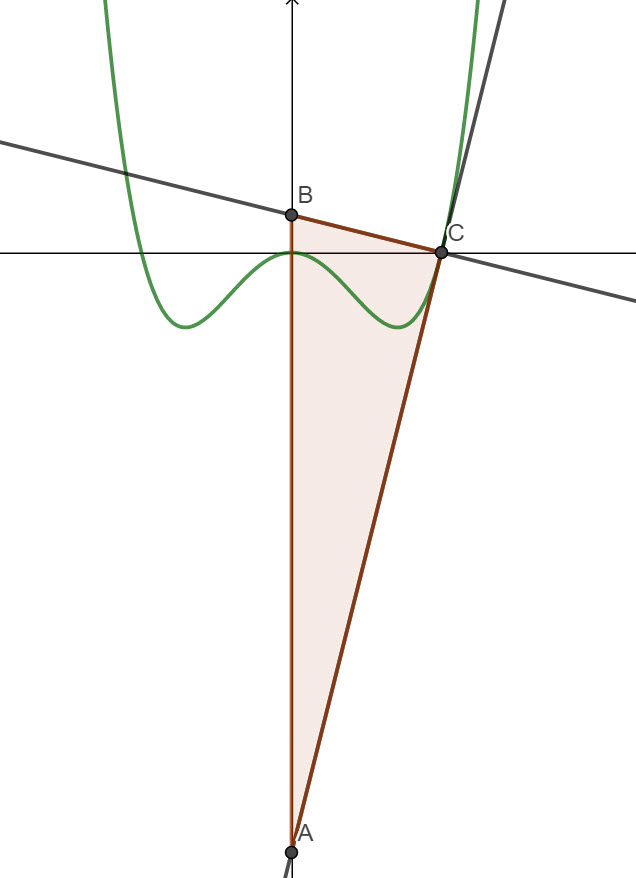
Let \(f(x)=\frac{x^4-4x^2}{4}\) .
C(2 , 0) lies on the graph of y = f(x)
a) The tangent to the graph of y = f(x) at C cuts the y axis at A. Find the coordinates of A.
b) The normal to the graph of y = f(x) at C cuts the y axis at B. Find the area of the triangle ABC.
Hint
It helps to visualise the problem
Full Solution
Print from here

The function \(f(x)=x^3-x^2-9x+9\) intersects the x axis at A, B and C.
The x coordinate of the point D is the mean of the x coordinates of B and C.
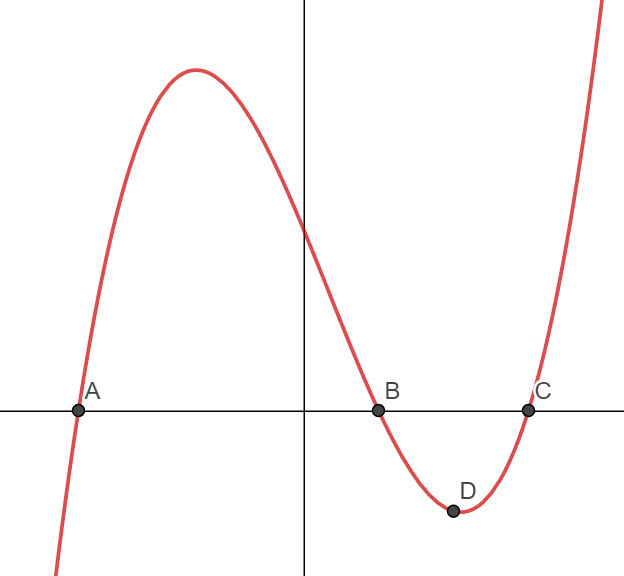
a) Find the coordinates of A, B and C.
b) Find the equation of the tangent to the curve at D.
c) Find the point of the intersection of the tangent with the curve. Interpret your result.
Hint
a) Use the Factor Theorem to find the coordinates of A, B and C
Full Solution
Print from here


A container is made from a cylinder and a hemisphere. The radius of the cylinder is r m and the height is h. The volume of the container is \(45\pi\)
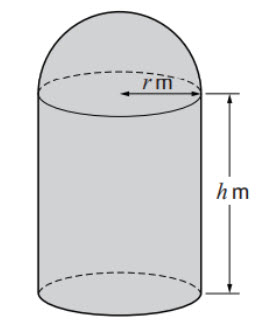
a) Find an expression for the height of the cylinder in terms of r
b) Show that the surface area of the container, \(A=\frac{5 \pi r^2}{3}+\frac{90 \pi}{r}\)
c) Hence, find the values of r and h that give the minimum surface area of the container
* Volume of a sphere = \(\frac{4}{3}\pi r^3\)
** Surface area of a sphere = \(4\pi r^2\)
Hint
The volume of a hemisphere = \(\frac{2}{3}\pi r^3\)
The curved surface area of a hemisphere = \(2\pi r^2\)
The surface area of the container = \(2\pi r^2+\pi r^2+2\pi rh\)
Full Solution
a) The volume of a hemisphere = \(\frac{2}{3}\pi r^3\)
The volume of the cylinder = \(\pi r^2h\)
Hence, the volume of the container = \(\frac{2}{3}\pi r^3+\pi r^2h\)
\(\frac{2}{3}\pi r^3+\pi r^2h=45\pi\)
We can divide through by \(\pi\) and rearrange to make h the subject of the formula
\(\frac{2}{3} r^3+ r^2h=45\)
\(r^2h=45-\frac{2}{3} r^3\)
\(h=\frac{45}{r^2}-\frac{2}{3} r\)
b) The surface area of the container = \(2\pi r^2+\pi r^2+2\pi rh\)
\(A=3\pi r^2+2\pi rh\)
\(A=3\pi r^2+2\pi r(\frac{45}{r^2}-\frac{2}{3} r)\)
\(A=\frac{9\pi r^2}{3}-\frac{4 \pi r^2}{3}+\frac{90 \pi}{r}\)
\(A=\frac{5\pi r^2}{3}+\frac{90 \pi}{r}\)
c) \(\frac{dA}{dr}=\frac{10\pi r}{3}-\frac{90 \pi}{r^2}\)
Minimimum occurs when \(\frac{dA}{dr}=0\)
\(\frac{10\pi r}{3}-\frac{90 \pi}{r^2}=0\)
\(\frac{10\pi r}{3}=\frac{90 \pi}{r^2}\)
\(r^3=27\)
r = 3
\(h=\frac{45}{3^2}-\frac{2}{3} \times 3\)
h = 5 - 2
h = 3
We can verify that this gives the minimum value by finding the 2nd derivative
\(\frac{dA}{dr}=\frac{10\pi r}{3}-\frac{90 \pi}{r^2}\)
\(\frac{d^2A}{dr^2}=\frac{180 \pi}{r^3}\)
When r = 3, \(\frac{d^2A}{dr^2}>0\) , hence A is a minimum


The diagram below shows the graph of the functions f(x) = sinx and g(x) = 2sinx
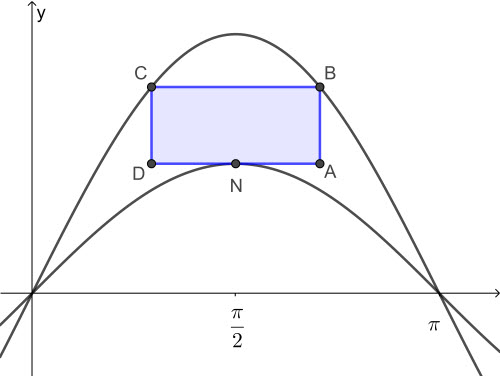
A rectangle ABCD is placed in between the two functions as shown so that B and C lie on g , BC is parallel to the x axis and the local minima of the function f lies on AD.
Let NA = x
a) Find an expression for the height of the rectangle AB
b) Show that the area of the rectangle, A can be given by A = 4xcosx - 2x
c) Find \(\frac{dA}{dx}\)
d) Find the maximum value of the area of the rectangle.
Hint
a) The y coordinate of B is \(g(\frac{\pi}{2}+x)=2sin(\frac{\pi}{2}+x)\)
b) Note that \(sin(x+\frac{\pi}{2})=cosx\)
Full Solution
a) The y cordinate of A is 1 (the maximum value of the function f(x) = sinx)
The y coordinate of B is \(g(\frac{\pi}{2}+x)=2sin(\frac{\pi}{2}+x)\)
The height of the rectangle, AB = \(2sin(\frac{\pi}{2}+x)-1\)
Note that \(sin(x+\frac{\pi}{2})=cosx\)
Therfore, AB = 2cosx - 1
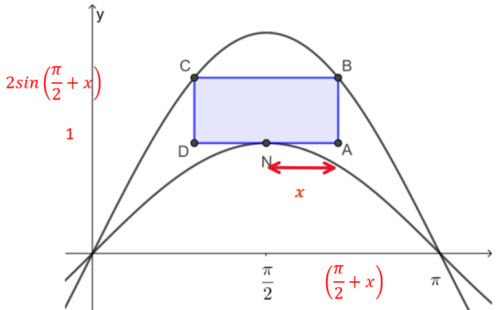
b) The width of the rectangle = 2x
Hence, the area of the rectangle, A = 2x(2cosx - 1) = 4xcosx - 2x
c) To find \(\frac{dA}{dx}\), we need to use the Product Rule
\(\frac{dA}{dx}=4cosx - 4xsinx - 2\)
d) The maximum value of the area of the rectangle occurs where \(\frac{dA}{dx}=0\)
We can use our graphical calculator to solve this. The value occurs when x \(\approx\) 0.592
Amax \(\approx\) 0.781

Find the equation of the tangent to the curve \(x^3 + y^3 -6xy = 0\) at the point (3,3)
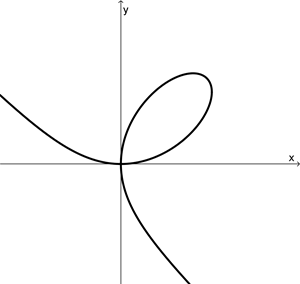
Hint
This is a question about implicit differentiation.
Differentiate \(x^3 + y^3 -6xy = 0\) with respect to x and find the gradient function
Full Solution
\(3x^2 +3y^2 \frac{dy}{dx} – (6y + 6x \frac{dy}{dx}) = 0\)
Substitute x=3 and y=3 to find the gradient of the tangent
\(3\times3^2 +3\times3^2 \frac{dy}{dx} – (6 \times3+ 6\times3 \frac{dy}{dx} ) = 0 \)
\(27 +27 \frac{dy}{dx} – (18+ 18 \frac{dy}{dx}) = 0\)
\(9 \frac{dy}{dx} +9 = 0\)
Our question becomes: find the equation of the tangent with gradient -1 which passes through the point (3,3)
\(-1=\frac{y-3}{x-3}\)
\(-x+3=y-3\)
\(y=-x+6\)

Find the gradient of the curve \(x^2+2e^{(x+2y)}=3\) at the point when x=-1
Hint
This is a question about implicit differentiation.
You will need to find the y coordinate when x=-1 and then find \(\frac{dy}{dx} \) at this point.
To find \(\frac{dy}{dx} \) , differentiate \(x^2+2e^{(x+2y)}=3\) with respect to x.
From the Chain Rule, we know that \(\frac{d}{dx}(e^{f(x)})=f'(x)e^{f(x)}\)
Full Solution
Substitute x=-1 into equation
\((-1)^2+2e^{(-1+2y)}=3\\ 1+2e^{(-1+2y)}=3\\ 2e^{(-1+2y)}=2\\ e^{(-1+2y)}=1\\ -1+2y=0\\ y=0.5\\ \)Find \(\frac{dy}{dx}\) by differentiating \( x^2+2e^{(x+2y)}=3\) with respect to x
From the Chain Rule, we know that \(\frac{d}{dx}(e^{f(x)})=f'(x)e^{f(x)}\)
\(2x+2(1+2\frac{dy}{dx})e^{(x+2y)}=0\)
Substitute x=-1, y=0.5
\(2(-1)+2(1+2\frac{dy}{dx})e^{(-1+2(0.5)}=0\\ -2+2(1+2\frac{dy}{dx})e^{(0)}=0\\ 2(1+2\frac{dy}{dx})=2\\ 1+2\frac{dy}{dx}=1\\ 2\frac{dy}{dx}=0\\ \frac{dy}{dx}=0 \)

A curve is defined by \(x\arcsin y=e^{2y}\)
Show that \(\frac{dy}{dx}=\frac{\sqrt{1-y^{2}}\arcsin y}{2e^{2y}\sqrt{1-y^{2}}-x}\)
Hint
This is a question about implicit differentiation.
Differentiate \(x\arcsin y=e^{2y}\) with respect to x and find the gradient function.
You might need to look up \(\frac{d}{dx}( arcsin x)\) in the information booklet.
You will need to use the Product Rule, since \(x\arcsin y\) is the product of two functions.
Careful rearrangement will be required!
Full Solution
Note that \(\frac{d}{dx}(\arcsin x)=\frac{1}{\sqrt{1-x^{2}}}\)
Therefore, \(\frac{d}{dx}(\arcsin y)=\frac{1}{\sqrt{1-y^{2}}}\frac{dy}{dx}\)
Differentiate \(x\arcsin y=e^{2y}\) with respect to x
\(1\arcsin y+x\frac{1}{\sqrt{1-y^{2}}}\frac{dy}{dx}=2e^{2y}\frac{dy}{dx}\)
Rearrange the equation to collect terms with \(\frac{dy}{dx}\) on one side
\(x\frac{1}{\sqrt{1-y^{2}}}\frac{dy}{dx}-2e^{2y}\frac{dy}{dx}=-\arcsin y\)
Multiply both sides by -1
\(2e^{2y}\frac{dy}{dx}-x\frac{1}{\sqrt{1-y^{2}}}\frac{dy}{dx}=\arcsin y\)
Factorise
\((2e^{2y}-\frac{x}{\sqrt{1-y^{2}}})\frac{dy}{dx}=\arcsin y\)
Divide both sides through by \(2e^{2y}-\frac{x}{\sqrt{1-y^{2}}}\)
\(\frac{dy}{dx}=\frac{\arcsin y}{2e^{2y}-\frac{x}{\sqrt{1-y^{2}}}}\)
Multiply numerator and denominator by \({\sqrt{1-y^{2}}}\)
\(\frac{dy}{dx}=\frac{\sqrt{1-y^{2}}\arcsin y}{2e^{2y}\sqrt{1-y^{2}}-x}\)

- Find the coordinates of the stationary point on the graph \(x^2y+2x=1\)
- Show that \(2y + 4x\frac{dy}{dx}+ x^2\frac{d^2y}{dx^2}=0\) and hence justify that the stationary point is a local minima.
Hint
This is a question about implicit differentiation. If you need a reminder about stationary points visit stationary points page
a) Differentiate \(x^2y+2x=1\) with respect to x. The stationary point exists where \( \frac{dy}{dx}=0\). You can find an equation for y in terms of x by substituting this into your equation. Can you use this and the initial equation to find the coordinates?
b) Differentiate the equation for a second time. Remember that local minima occurs when \(\frac{d^2y}{dx^2}>0 \)
Full Solution
a)
Differentiate \(x^2y+2x=1\) with respect to x.
\(2xy + x^2\frac{dy}{dx}+2=0\)
Substitute \(\frac{dy}{dx}=0 \)
\(2xy + 0 + 2 = 0\)
\(xy = -1\)
\(y = \frac{-1}{x}\)
Substitute \(y = \frac{-1}{x}\) into initial implicit equation.
\(x^2(\frac{-1}{x})+2x=1\\ -x + 2x = 1\\ x=1\\ y=-1 \)
Hence, a stationary point exists at (1, -1)
b)
\(2xy + x^2\frac{dy}{dx}+2=0\)
Differentiate \(2xy + x^2\frac{dy}{dx}+2=0\) with respect to x
\(2y + 2x\frac{dy}{dx}+ 2x\frac{dy}{dx}+ x^2\frac{d^2y}{dx^2}=0\)
Hence
\(2y + 4x\frac{dy}{dx}+ x^2\frac{d^2y}{dx^2}=0\)
Substitute x=1 , y= -1, \(\frac{dy}{dx}=0\)
\(-2 + 0 + \frac{d^2y}{dx^2}=0\\ \frac{d^2y}{dx^2}=2 \)
Since \(\frac{d^2y}{dx^2}>0\) , stationary point at (1, -1) is a local minima

The radius of a sphere is increasing at 2.5 cms-1
Find the rate at which the volume of the sphere is increasing when the radius is 8 cm.
Give your answer in terms of \(\large \pi\)
Hint
The rate at which the volume of the sphere is increasing is \(\large \frac{dV}{dt}\)
To find it, use the chain rule
\(\large \frac{dV}{dt}=\)\(\large \frac{dV}{dr}\)\(\large \times\)\(\large \frac{dr}{dt}\)
Full Solution
The volume of a sphere, \(\large V = \frac{4}{3}\pi r^3\)
Differentiate with respect to r , \(\large \frac{dV}{dr}=4\pi r^2\)
When r = 8 cm , \(\large \frac{dV}{dr}=4\pi \times 8^2=256 \pi\)
The radius of a sphere is increasing at 2.5 cms-1, \(\large \frac{dr}{dt}=2.5\)
Using the chain rule
\(\large \frac{dV}{dt}=\)\(\large \frac{dV}{dr}\)\(\large \times\)\(\large \frac{dr}{dt}\)
\(\large \frac{dV}{dt}=\)\(\large 256 \pi\)\(\large \times\)\(\large 2.5\)
\(\large \frac{dV}{dt}=640 \pi\)

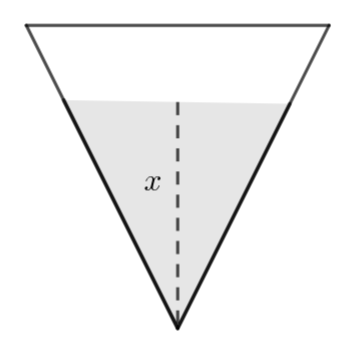 The diagram shows a container in the form of a right circular cone. The height of the cone is equal to its diameter. Initially the cone is empty, then water is added at a rate of \(\large 18\pi\) cm3 per minute. the depth of water in the container at the time is given by h cm.
The diagram shows a container in the form of a right circular cone. The height of the cone is equal to its diameter. Initially the cone is empty, then water is added at a rate of \(\large 18\pi\) cm3 per minute. the depth of water in the container at the time is given by h cm.
a) Show that the volume, V cm3 , of water in the container when the depth is x cm is given by
\(\large V=\frac{1}{12} \pi x^3\)
b) Find the rate at which the depth of the water is increasing at the instant when the depth is 12 cm
Hint
a) height = diameter
Therefore, \(\large r=\frac{h}{2}\)
In this case, the height of water = x
b) The rate at which the depth of the water is increasing is \(\large \frac{dx}{dt}\)
To find it, use the chain rule
\(\large \frac{dV}{dt}\)=\(\large \frac{dV}{dx}\)\(\large \times\)\(\large \frac{dx}{dt}\)
Full Solution
a) The volume of a cone, \(\large V = \frac{1}{3}\pi r^2h\)
In this case the height = diameter
Therefore, \(\large r=\frac{h}{2}\)
The volume of a cone, \(\large V = \frac{1}{3}\pi (\frac{h}{2})^2h\\ \large V = \frac{1}{3}\pi (\frac{h^2}{4})h\\ \large V = \pi \frac{h^3}{12}\)
When the depth (height) of water= x, then
\(\large V=\frac{1}{12} \pi x^3\)
b) \(\large V=\frac{1}{12} \pi x^3\)
Differentiate with respect to x , \(\large \frac{dV}{dx}=\frac{1}{4}\pi r^2\)
When x = 12 cm , \(\large \frac{dV}{dx}=\frac{1}{4}\pi \times12^2=36\pi\)
Water is added at a rate of \(\large 18\pi\) cm3 per minute, \(\large \frac{dV}{dt}=18 \pi\)
Using the chain rule
\(\large \frac{dV}{dt}\)=\(\large \frac{dV}{dx}\)\(\large \times\)\(\large \frac{dx}{dt}\)
\(\large 18 \pi\) =\(\large36\pi\)\(\large \times\)\(\large \frac{dx}{dt}\)
\(\large \frac{dx}{dt}=\frac{18\pi}{36\pi}\)
\(\large \frac{dx}{dt}=0.5\) cm per minute

A searchlight rotates at 2 revolutions per minute. The beam hits a wall 30m away and produces a spot of light that moves horizontally along the wall. How fast is the spot moving along the wall when the angle, \(\large \theta\) between the beam and the line through the spotlight perpendicular to the wall is 45°?
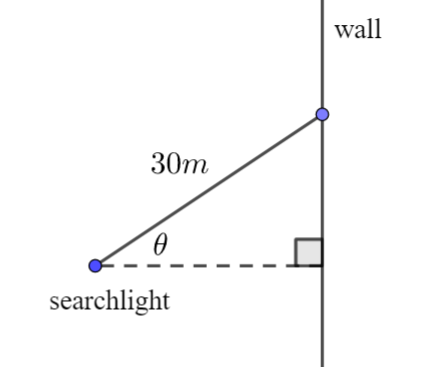
Hint
If we let x be the distance along the wall, then the speed of the spotlight is\(\large \frac{dx}{dt}\)
To find it, use the chain rule
\(\large \frac{dx}{dt}\)=\(\large \frac{dx}{d\theta}\)\(\large \times\)\(\large \frac{d\theta}{dt}\)
To find \(\large \frac{dx}{d\theta}\) use right-angled triangle trigonometry to find x in terms of \(\large \theta\)
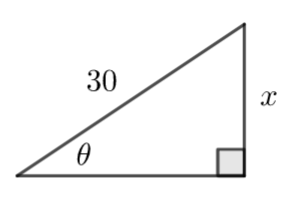
Full Solution
The searchlight is rotating at 2 revolutions per minute
1 revolution is \(\large 2\pi \) radians
Therefore, \(\large \frac{d\theta}{dt}=4\pi\) radians per minute
Let the distance fom from the perpendicular be x

\(\large \sin \theta=\frac{x}{30}\)
\(\large x=30 \sin\theta\)
Differentiate with respect to \(\large \theta\)
\(\large \frac{dx}{d\theta}=30 \cos \theta\)
When \(\theta\)=45°, \(\large \frac{dx}{d\theta}=30 \cos45°=15\sqrt{2}\)
Use the chain rule
\(\large \frac{dx}{dt}\)=\(\large \frac{dx}{d\theta}\)\(\large \times\)\(\large \frac{d\theta}{dt}\)
\(\large \frac{dx}{dt}\)=\(\large 15\sqrt{2}\)\(\large \times\)\(\large 4\pi\)
\(\large \frac{dx}{dt}=60\sqrt{2}\pi\approx267\)m per minute

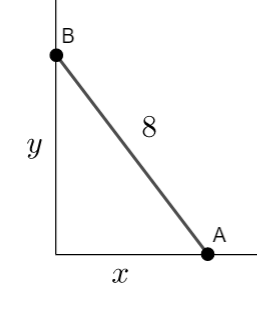
A ladder AB of length 8m has one endA on horizontal ground and the other end B resting against a vertical wall.
The end A slips away from the wall at a constant speed of 0.5 ms-1 and the end B slips down the wall.
Determine the speed of the end B is slipping down the wall when the top of the ladder is 5 m above the ground.
Hint
If we let x be the distance along the ground, then the speed end A slips away from the wall is \(\large \frac{dx}{dt}\)
If w let y be the distance up the wall, then the speed end B slips down the wall is \(\large \frac{dy}{dt}\)
Use Pythagoras' Theorem
Full Solution
The speed end A slips away from the wall is \(\large \frac{dx}{dt}\)
\(\large \frac{dx}{dt}=0.5\) ms-1
The speed end B slips down the wall is \(\large \frac{dy}{dt}\)
Using Pythagoras' Theorem
\(\large x^2+y^2=8^2\)
\(\large x^2+y^2=64\)
Differentiate with respect to t (implicit differentiation)
\(\large 2x \frac{dx}{dt}+2y\frac{dy}{dt}=0\)
When y =5 ,
\(\large x^2+5^2=64\\ \large x^2=39\\ \large x=\sqrt {39}\)
Substitute these values in the differential equation
\(\large 2x \frac{dx}{dt}+2y\frac{dy}{dt}=0\)
\(\large 2\sqrt{39}\times 0.5+2\times 5\frac{dy}{dt}=0\\ \large 10\frac{dy}{dt}=-\sqrt{39}\\ \large \frac{dy}{dt}=-\frac{\sqrt{39}}{10}\\ \large \frac{dy}{dt}=-0.624\)
Notice that the value is negative. This represents the velocity and shows that it is slipping down.
The speed is 0.624 ms-1

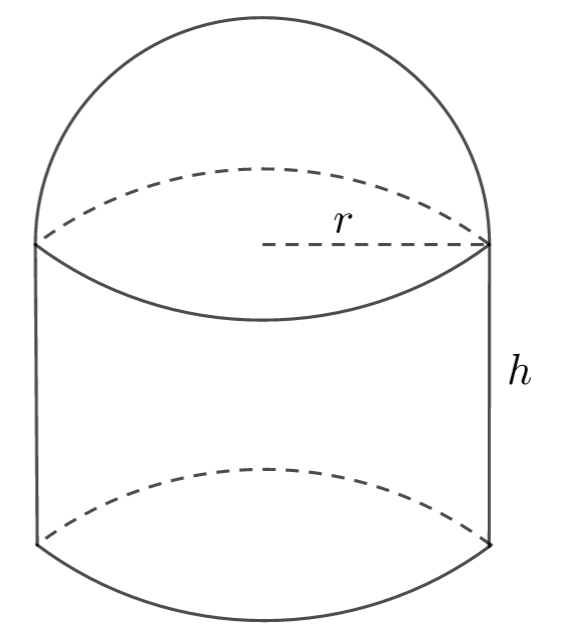
A solid is made up of a cylinder and a hemisphere as shown in the diagram.
a) Write down a formula for the volume of the solid.
b) At the time when the radius is 6cm, the volume of the solid is \(\large 684\pi\) cm3 , the radius is changing at a rate of 1.5 cm/minute and the volume is changing at a rate of \(\large 1800\pi\) cm3 /min. Find the rate of change of the height at this time.
Hint
We can find the volume of the solid to be \(\large V=\frac{2}{3}\pi r^3+\pi r^2h\)
We know \(\large \frac{dr}{dt}\) and \(\large \frac{dV}{dt}\). We are required to find \(\large \frac{dh}{dt}\).
Use implicit differentiation and differentiate the formula for V with respect to t
Full Solution
a) The volume of a hemisphere is \(\large \frac{2}{3}\pi r^3\)
The volume of a cylinder is \(\large \pi r^2h\)
The volume of the solid, \(\large V=\frac{2}{3}\pi r^3+\pi r^2h\)
b) We can find the value of h when r = 6 and V = \(\large 684\pi\)
\(\large 684\pi=\frac{2}{3}\pi \times 6^3+\pi \times 6^2\times h\\ \large 684\pi=144\pi+36\pi h\\ \large 540\pi=36\pi h\\ \large h = 15\)
The radius is changing at a rate of 1.5 cm/minute, \(\large \frac{dr}{dt}=1.5\)
The volume is changing at a rate of \(\large 1800\pi\) cm3 /min, \(\large \frac{dV}{dt}=1800\pi\)
We are required to find \(\large \frac{dh}{dt}\).
Use implicit differentiation and differentiate the formula for V with respect to t
\(\large V=\frac{2}{3}\pi r^3+\pi r^2h\)
Notice that the second part of the expression 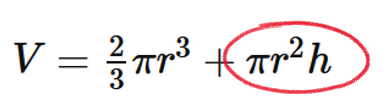 is a product (both r and h are variables). Therefore we need to use the Product Rule for differentiation
is a product (both r and h are variables). Therefore we need to use the Product Rule for differentiation
\(\large \frac{dV}{dt}=2\pi r^2\frac{dr}{dt}+\pi r^2\frac{dh}{dt}+2\pi r^2\frac{dr}{dt}\cdot h\)
\(\large 1800\pi=2\pi \times 6^2\times 1.5+\pi \times 6^2\frac{dh}{dt}+2\pi \times 6^2\times 1.5\times 15\\ \large 1800\pi=108\pi+36\pi \cdot \frac{dh}{dt}+1620\pi\\ \large 72\pi=36\pi \cdot \frac{dh}{dt}\\ \large \frac{dh}{dt}=2\)
\(\large \frac{dh}{dt}=2\) cm/min

Use l’Hôpital’s rule to determine the value of \(\large \lim\limits_{x\rightarrow 0}( x \ln x)\)
Hint
Full Solution
\(\large \lim\limits_{x\rightarrow 0} (x \ln x)= \lim\limits_{x\rightarrow 0} \frac{\ln x}{\frac{1}{x}}=\frac{-\infty}{\infty}\)
This is in the indeterminate form
Let \(\large f(x) = \ln x\) and \(\large g(x) = x^{-1}\)
Then, \(\large f'(x) = \frac{1}{x}\) and \(\large g'(x) = -x^{-2}=-\frac{1}{x^2}\)
Therefore,
\( \lim\limits_{x\rightarrow 0} \frac{\ln x}{\frac{1}{x}}= \lim\limits_{x\rightarrow 0} \frac{\frac{1}{x}}{-\frac{1}{x^2}}\)
We can simplify this
\(\lim\limits_{x\rightarrow 0} \frac{\frac{1}{x}}{-\frac{1}{x^2}}=\lim\limits_{x\rightarrow 0} \frac{-x^2}{x}=\lim\limits_{x\rightarrow 0}(-x)=0\)
Therefore, \(\large \lim\limits_{x\rightarrow 0} (x \ln x)= 0\)

Use l’Hôpital’s rule to determine the value of \(\large \lim\limits_{x\rightarrow 0}\frac{e^{x^2}-1}{\sin x^2}\)
Hint
Full Solution
\(\large \lim\limits_{x\rightarrow 0}\frac{e^{x^2}-1}{\sin x^2}=\frac{1-1}{0}=\frac{0}{0}\)
This is in the indeterminate form
Let \(\large f(x) = e^{x^2}-1\) and \(\large g(x) =\sin x^2\)
Then, \(\large f'(x) = 2xe^{ x^2}\) and \(\large g'(x) = 2x\cos x^2\)
Therefore,
\(\large \lim\limits_{x\rightarrow 0}\frac{e^{x^2}-1}{\sin x^2}= \lim\limits_{x\rightarrow 0}\frac{2xe^{x^2}}{2x\cos x^2}\)
We can simplify this
\(\large \lim\limits_{x\rightarrow 0}\frac{e^{x^2}}{\cos x^2}=\frac{1}{1}=1\)

Use l’Hôpital’s rule to determine the value of \(\large \lim\limits_{x\rightarrow 0}\frac{1-\cos x^2}{x^4}\)
Hint
The second application will need simplifying
Full Solution
\(\large \lim\limits_{x\rightarrow 0}\frac{1-\cos x^2}{x^4}=\frac{1-1}{0}=\frac{0}{0}\)
This is in the indeterminate form
Let \(\large f(x) = 1-\cos x^2\) and \(\large g(x) = x^4\)
Then, \(\large f'(x) = 2x\sin x^2\) and \(\large g'(x) = 4x^3\)
Therefore,
\(\large \lim\limits_{x\rightarrow 0}\frac{1-\cos x^2}{x^4}= \lim\limits_{x\rightarrow 0}\frac{2x\sin x^2}{4x^3}\)
We can simplify this
\(\large \lim\limits_{x\rightarrow 0}\frac{\sin x^2}{2x^2}=\frac{0}{0}\)
We can apply l'Hôpital's rule again
Let \(\large f(x) = \sin x^2\) and \(\large g(x) = 2x^2\)
Then, \(\large f'(x) = 2x\cos x^2\) and \(\large g'(x) = 4x\)
Therefore, \(\large \lim\limits_{x\rightarrow 0}\frac{\sin x^2}{2x^2}= \lim\limits_{x\rightarrow 0}\frac{2x\cos x^2}{4x}\)
We can simplify this
\(\large \lim\limits_{x\rightarrow 0}\frac{\cos x^2}{2}=\frac{1}{2}\)
Therefore, \(\large \lim\limits_{x\rightarrow 0}\frac{1-\cos x^2}{x^4}=\frac{1}{2}\)

Use l’Hôpital’s rule to determine the value of \(\large \lim\limits_{x\rightarrow 0}\frac{6\tan x-6x}{x^3}\)
Hint
Ensure that you simplify the limit if it is possible.
Full Solution
\(\large \lim\limits_{x\rightarrow 0}\frac{6\tan x-6x}{x^3}=\frac{0-0}{0}=\frac{0}{0}\)
This is in the indeterminate form
Let \(\large f(x) = 6\tan x-6x\) and \(\large g(x) = x^3\)
Then, \(\large f'(x) = 6 \sec ^2x-6\) and \(\large g'(x) = 3x^2\)
Therefore,
\(\large \lim\limits_{x\rightarrow 0}\frac{6\tan x-6x}{x^3}= \lim\limits_{x\rightarrow 0}\frac{\frac{6}{(\cos x)^2}-6}{3x^2}=\frac{0}{0}\)
We can apply l'Hôpital's rule again
Let
\(\large f(x) = \frac{6}{(\cos x)^2}-6\\ \large f(x) =6(\cos x)^{-2}-6\) and \(\large g(x) = 3x^2\)
Then,
\(\large f'(x) =6(-2)(-\sin x)(\cos x)^{-3}\\ \large f'(x)=\frac{12\sin x}{(\cos x)^3}\) and \(\large g'(x) = 6x\)
Therefore, \(\large \lim\limits_{x\rightarrow 0}\frac{6\tan x-6x}{x^3}= \lim\limits_{x\rightarrow 0}\frac{\frac{12\sin x}{(\cos x)^3}}{6x}\)
We can simplify this
\(\large \lim\limits_{x\rightarrow 0}\frac{2\sin x}{x(\cos x)^3}\)
We can apply l'Hôpital's rule again
Let
\(\large f(x) = 2\sin x\) and \(\large g(x) = x(\cos x)^3\)
Then,
\(\large f'(x) =2\cos x\) and \(\large g'(x) = 1(\cos x)^3+x\cdot3(-\sin x)(\cos x)^2\\ \large g'(x) = (\cos x)^3-3x\sin x(\cos x)^2\)
Therefore, \(\large \lim\limits_{x\rightarrow 0}\frac{6\tan x-6x}{x^3}=\lim\limits_{x\rightarrow 0}\frac{2\cos x}{ (\cos x)^3-3x\sin x(\cos x)^2}=\frac{2}{1-0}=2\)
\(\large \lim\limits_{x\rightarrow 0}\frac{6\tan x-6x}{x^3}=2\)


Given that \(\int _{ 4 }^{ 8 }{ \frac { 1 }{ 2x-4 } dx= } ln\sqrt { a } \) , find the value of a
Hint
Full Solution
Print from here


Consider a function f(x) such that \(\int _{ 0 }^{ 4 }{ f(x)dx } \) = 6
Find
a) \(\int _{ 0 }^{ 4 }{3 f(x)dx } \)
b) \(\int _{ 0 }^{ 4 }{[ f(x)+3]dx } \)
c) \(\int _{ -3 }^{ 1 }{\frac{1}{3} f(x+3)dx } \)
d) \(\int _{ 0 }^{ 4 }{ [f(x)+x]dx } \)
Hint
\(\int _{ a }^{ b }{k f(x)dx } =k\int _{ a }^{ b }{ f(x)dx } \)
\(\int _{ a }^{ b }{ [f(x)+g(x)]dx } =\int _{ a }^{ b }{ f(x)dx } +\int _{ a }^{ b }{ g(x)dx } \)
Full Solution
Print from here


Given that \(\int _{ 2 }^{ 5 }{ ln(sinx)dx=A } \)
show that \(\int _{ 2 }^{ 5 }{ ln({ e }^{ x }sinx)dx=A } +\frac { 21 }{ 2 } \)
Hint
Full Solution
Print from here


Let f(x)=sinx, for \(0\le x\le 2\pi \)
The following diagram shows the graph of f
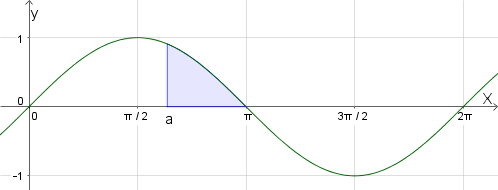
The shaded region R is enclosed by the graph of f, the line x=a , where a<\(\pi\) and the x-axis.
The area of R is \(\left( 1-\frac { \sqrt { 3 } }{ 2 } \right) \). Find the value of b.
Hint
Full Solution
Print from here


Show that the area bounded by the graphs of y = f(x) and y = g(x) in the interval \(0\le x\le \pi \) is given by 2 - \(\frac { \pi }{ 2} \)
f(x) = sinx
g(x) = sin²x
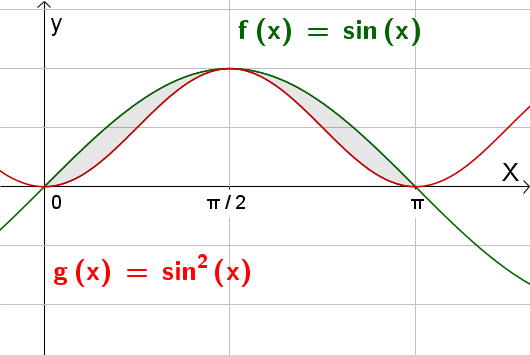
Hint
- You need to find the area between the two graphs y = sinx and y=sin²x
- The tricky part is integrating sin²x. To do this you will need to use the trig identity for cos2x
Full Solution
Print from here


Let \(f(x)=ln\left( \frac { x }{ x-1 } \right) \) for x>1
a) Find f ' (x)
b) Hence, show that the area bounded by g(x) = \(\frac { 1 }{ x(x-1) } \) , the x axis, x = 2 and x = e is given by \(ln\left( \frac { 2e-2 }{ e } \right) \)
Hint
b) 'Hence' is important here. This suggests that the way to do part b) follows from what you have found in part a). You should notice that the function to integrate is the same as the answer to part a)
Full Solution
Print from here

The graph below shows the function f(x) = sinx where a < b \(\le \frac { \pi }{ 2 } \)
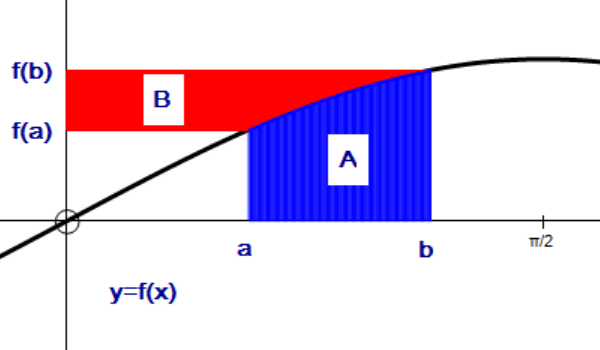
a) Write an expression for the area A, bounded by the curve y = f(x), the x axis, x = a and x = b
b) Hence, without using any further integration, show that the area B = \(bsinb - asina - cosb + cosa\)
c) Area B can also be found by finding the area bounded by the curve x = f(y), the y axis, y = f(a) and y = f(b). Find the area B using this method and show that your answer is the same as the one you found in part b)
Hint
c) Find the area bounded by x = arcsiny, y= sina, y= sinb and the y axis.
You can use integration by parts to find \(\int { 1\bullet \arcsin { y}_\ dy } \) . This method is similar to integrating lnx
You will then be required to find \(\int { \frac { y }{ \sqrt { 1-{ y }^{ 2 } } } dy } \) which you can do using the method of integration by substitution or recognition.
Full Solution

a) Area A
\(= \int _{ a }^{ b }{ sinx } dx\\ ={ [-cosx] }_{ a }^{ b }\\ =-cosb\ +\ cosa\)
b)
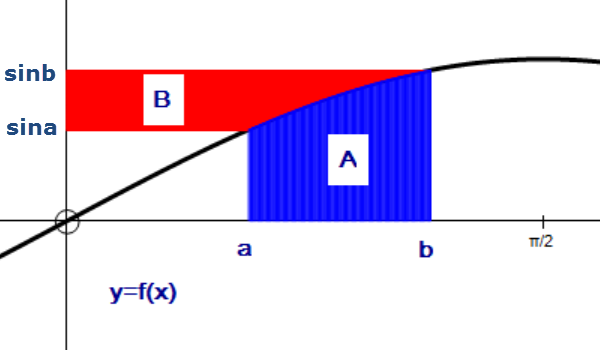
Area B = area large rectangle - area small rectangle - area A
= bsinB - a sinA - (-cosb + cosa)
= bsinB - a sinA + cosb - cosa
c) Graph is y = sinx which is equivalent to x = arcsiny for \(0\le \ x\le \frac { \pi }{ 2} \ \)
Area B \(=\int _{ sina }^{ sinb }{ \arcsin { y } }\ dy\)
Let's consider \(\int { \arcsin { y } }\ dy\)
We can use integration by parts
\(\int {u\frac{{dv}}{{dx}}}\ dx = uv - \int {\frac{{du}}{{dx}}}\ vdx\)
since our variable is y , this becomes
\(\int {u\frac{{dv}}{{dy}}} \ dy = uv - \int {\frac{{du}}{{dy}}} v \ dy\)
We make our integral a product of two parts (this is like integrating lnx)
\(\int 1\cdot { \arcsin { y } } \ dy\)
\(u = arcsiny \quad \frac { dv }{ dy } = 1\\ \frac { du }{ dy } = \frac { 1 }{ \sqrt { 1-{ y }^{ 2 } } }\quad v = y\\\)
\(=y \cdot arcsiny - \int \frac { y }{ \sqrt { 1-{ y }^{ 2 } } } \ dy\)
To find \(\int \frac { y }{ \sqrt { 1-{ y }^{ 2 } } } \ dy\) , we need to use integration by substitution (or recognition)
Let w = 1 - y2
\( \frac { dw }{dy } = -2y\)
\(=y \cdot arcsiny + \int \frac { 1 }{ 2 } { w }^{ -\frac { 1 }{ 2 } }\ dw\)
\(=y \cdot arcsiny + { w }^{ \frac { 1 }{ 2 } } \ +c\)
\(=y \cdot arcsiny + \sqrt {1-{ y }^2 } \ +c\)
So, let's go back to the area of B
Area B \(=\int _{ sina }^{ sinb }{ \arcsin { y } }\ dy\)
\(={ \left[ { \ y \cdot arcsiny + \sqrt {1-{ y }^2 } } \ \right] }_{ sina }^{ sinb }\)
\(=[\ sinb\cdot b+\sqrt { 1-sin²b } \ ]-[ \ sina\cdot a+\sqrt { 1-sin²a } \ ]\)
Since, 1-sin²x = cos²x
\(=[\ sinb\cdot b+cosb\ ]-[ \ sina\cdot a+cosa \ ]\)
\(= b\cdot sinb+cosb- \ a\cdot sina-cosa \)
= bsinB - a sinA + cosb - cosa
Volume of Revolution

a) Show that \(\large \int {x^2e^{2x}\,dx}=\frac{1}{4}e^{2x}(2x^2-2x+1)+c\)
The following graph shows the function \(\large f(x)=xe^x\)
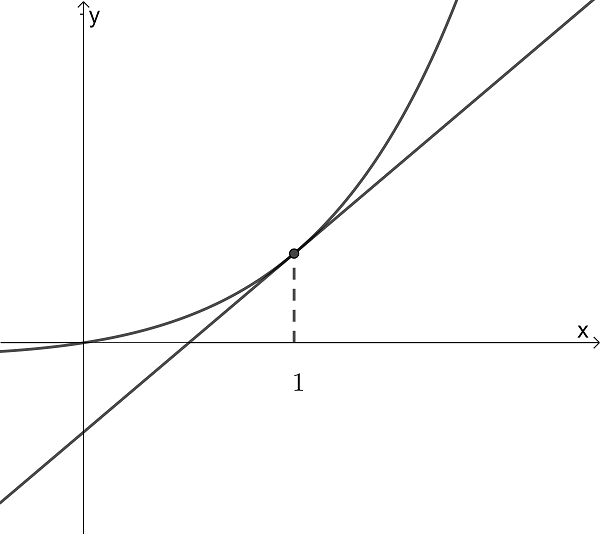
b) Show that the equation of the tangent to the graph at x = 1 has the equation \(\large y=(2e)x-e\)
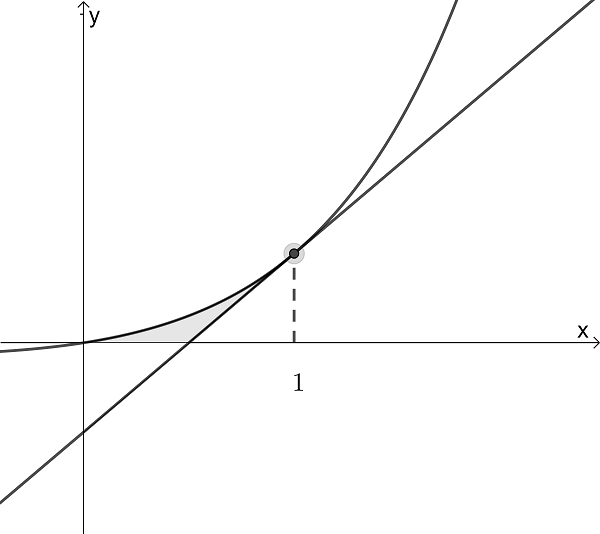
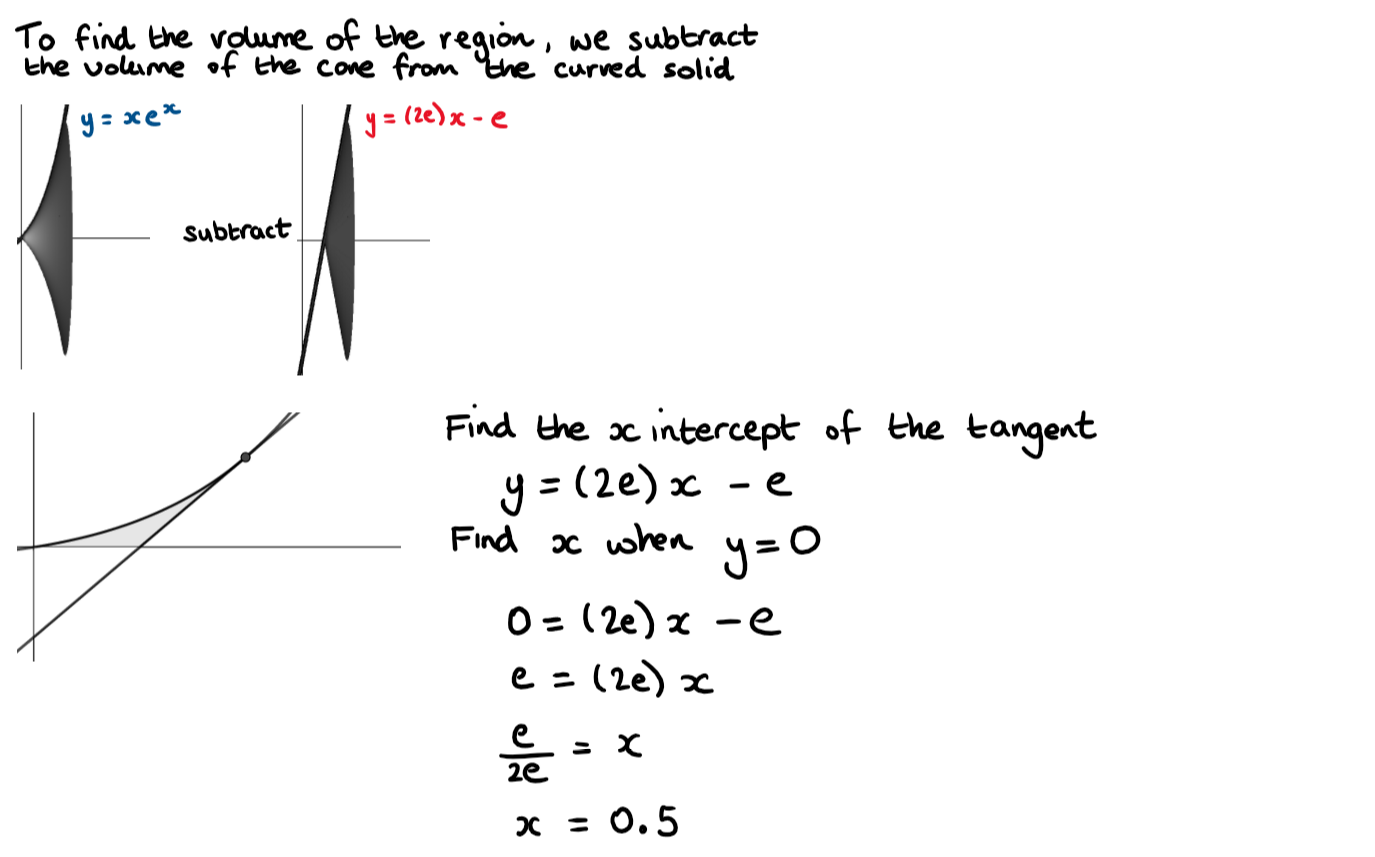
The region bounded by \(\large f\), the tangent \(\large y=(2e)x-e\) and y = 0 is rotated \(\large 2\pi\) around the x axis
c) Find the volume of this solid in terms of \(\large \pi\)
Hint
a) this is an integration by parts question
Full Solution
a)
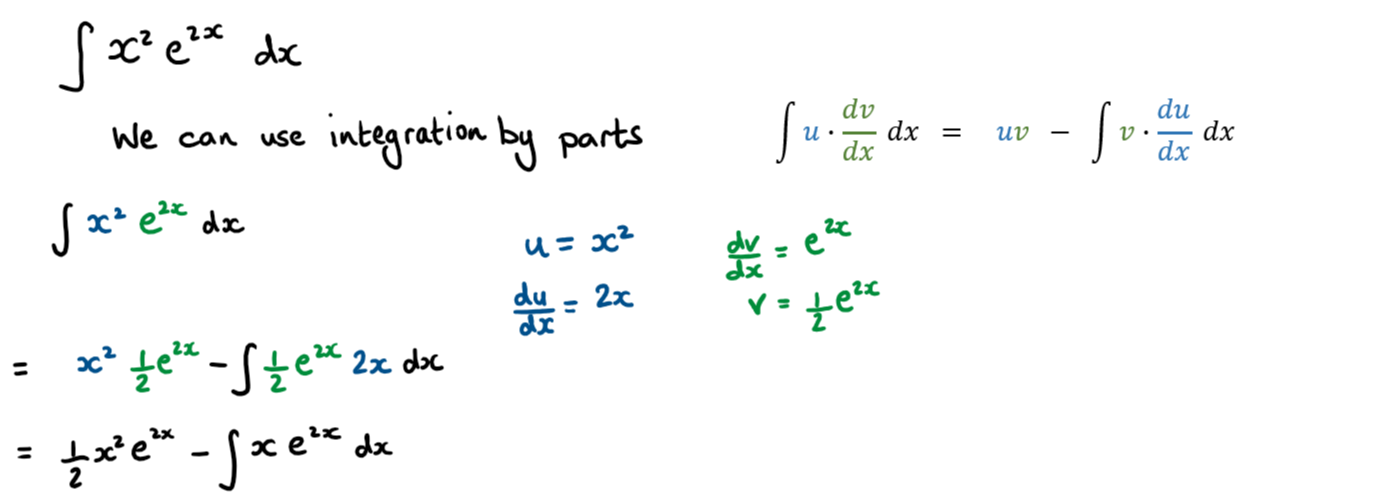

b)

c)
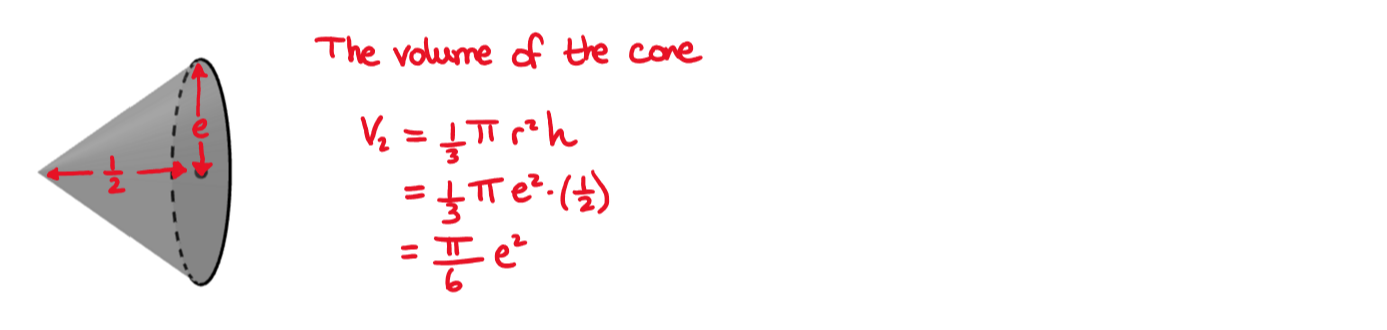
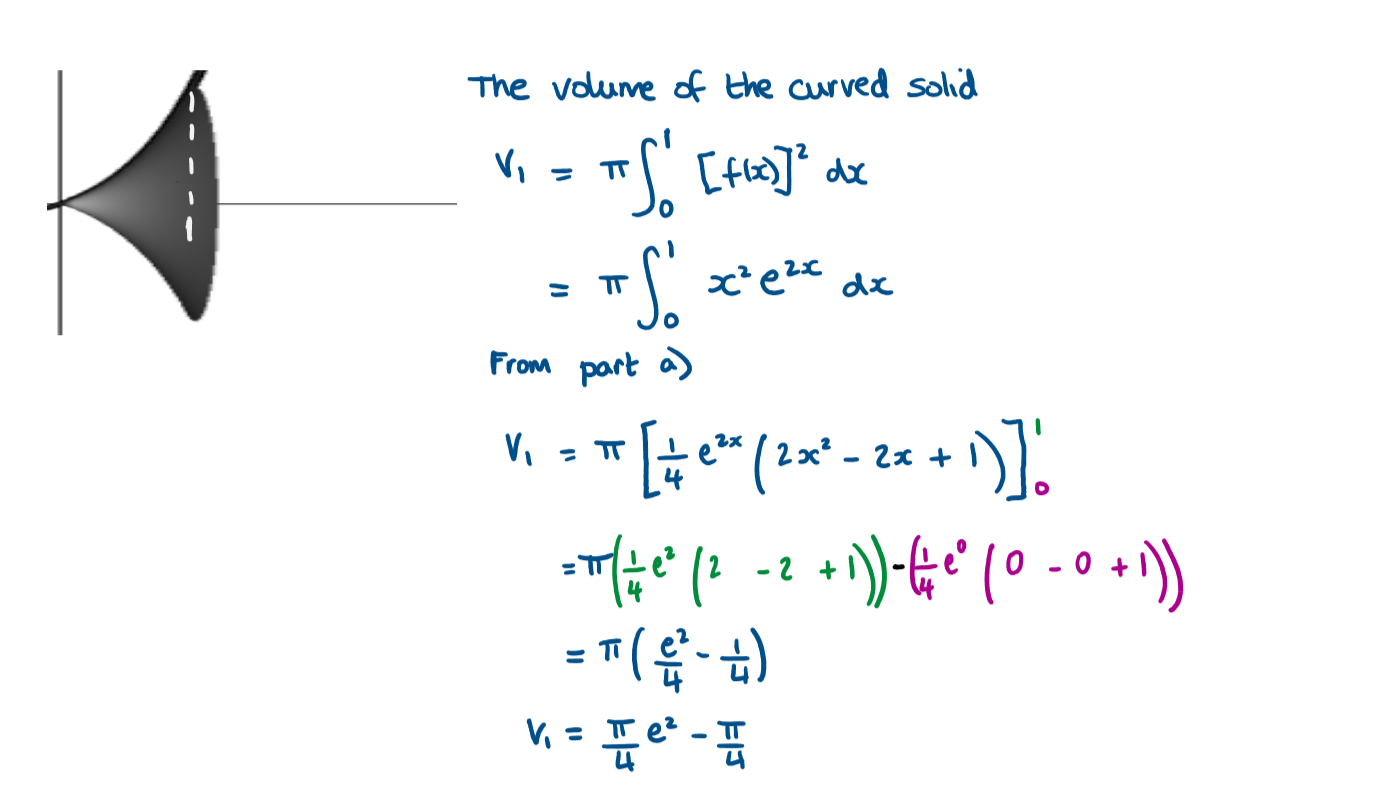


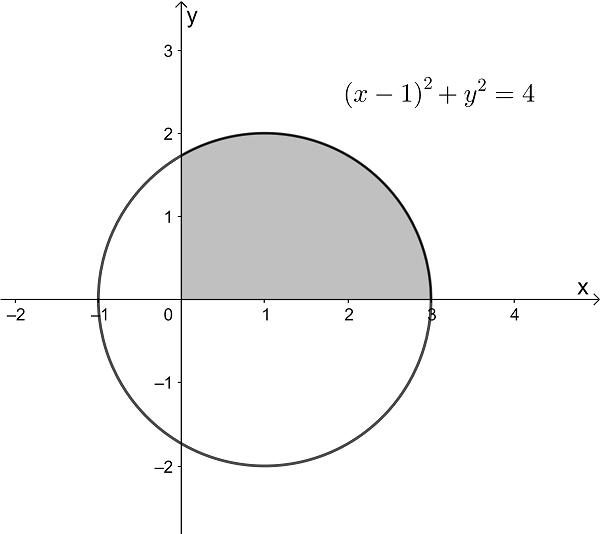
The following graph shows the curve defined by the equation \(\large (x-1)^2+y^2=4\).
The region bounded by the curve and the lines y = 0 and x = 0 is rotated \(\large 2\pi\) around the x axis.
Find the volume of this solid in terms of \(\large \pi\)
Hint
The volume of the solid is found using the formula
Full Solution
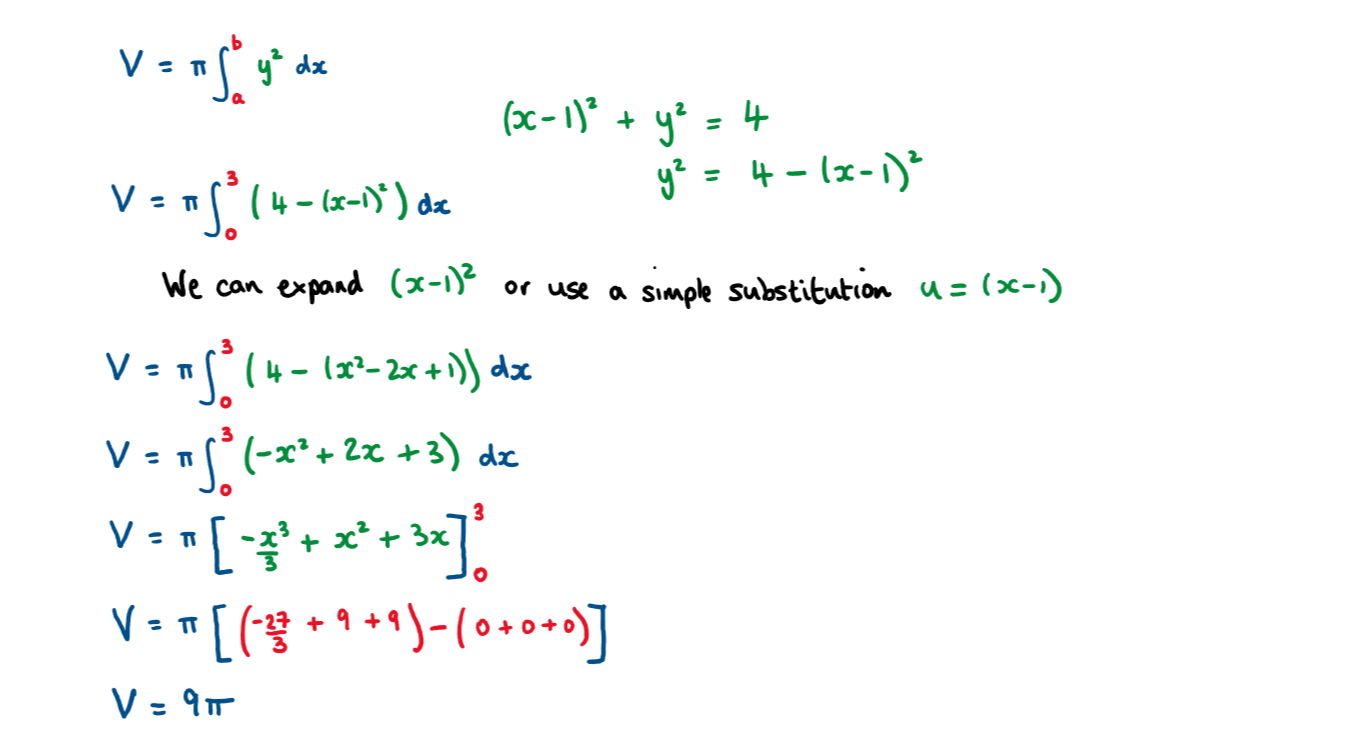

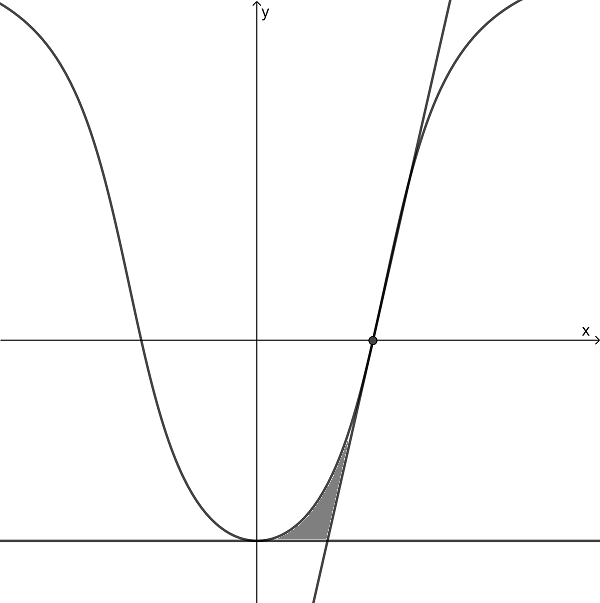
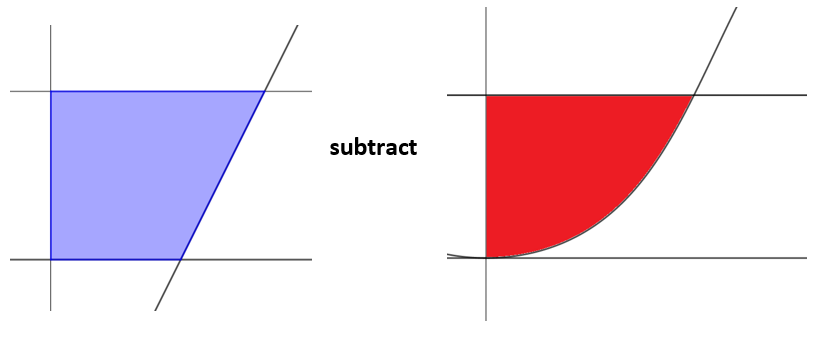
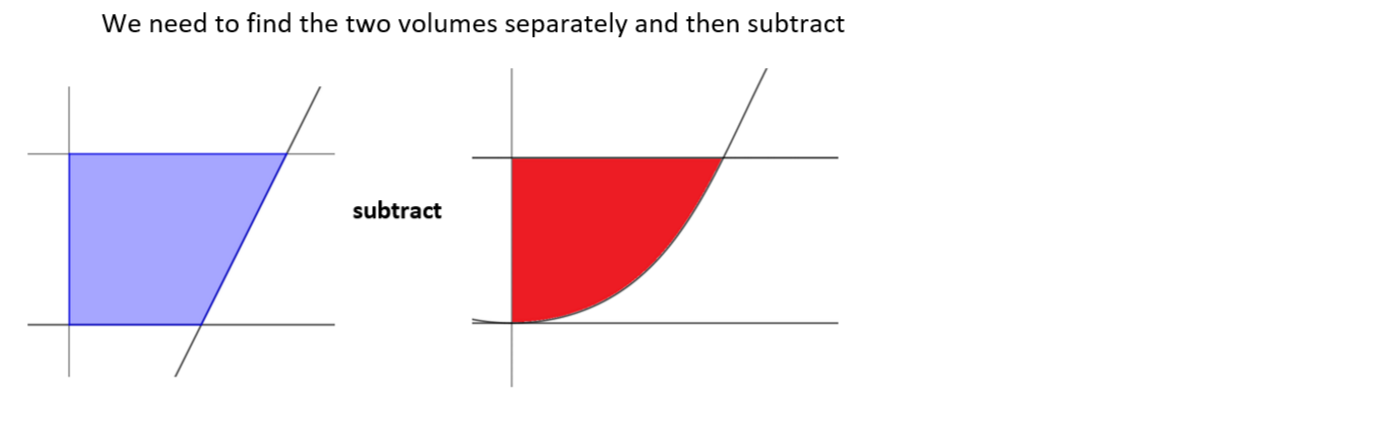
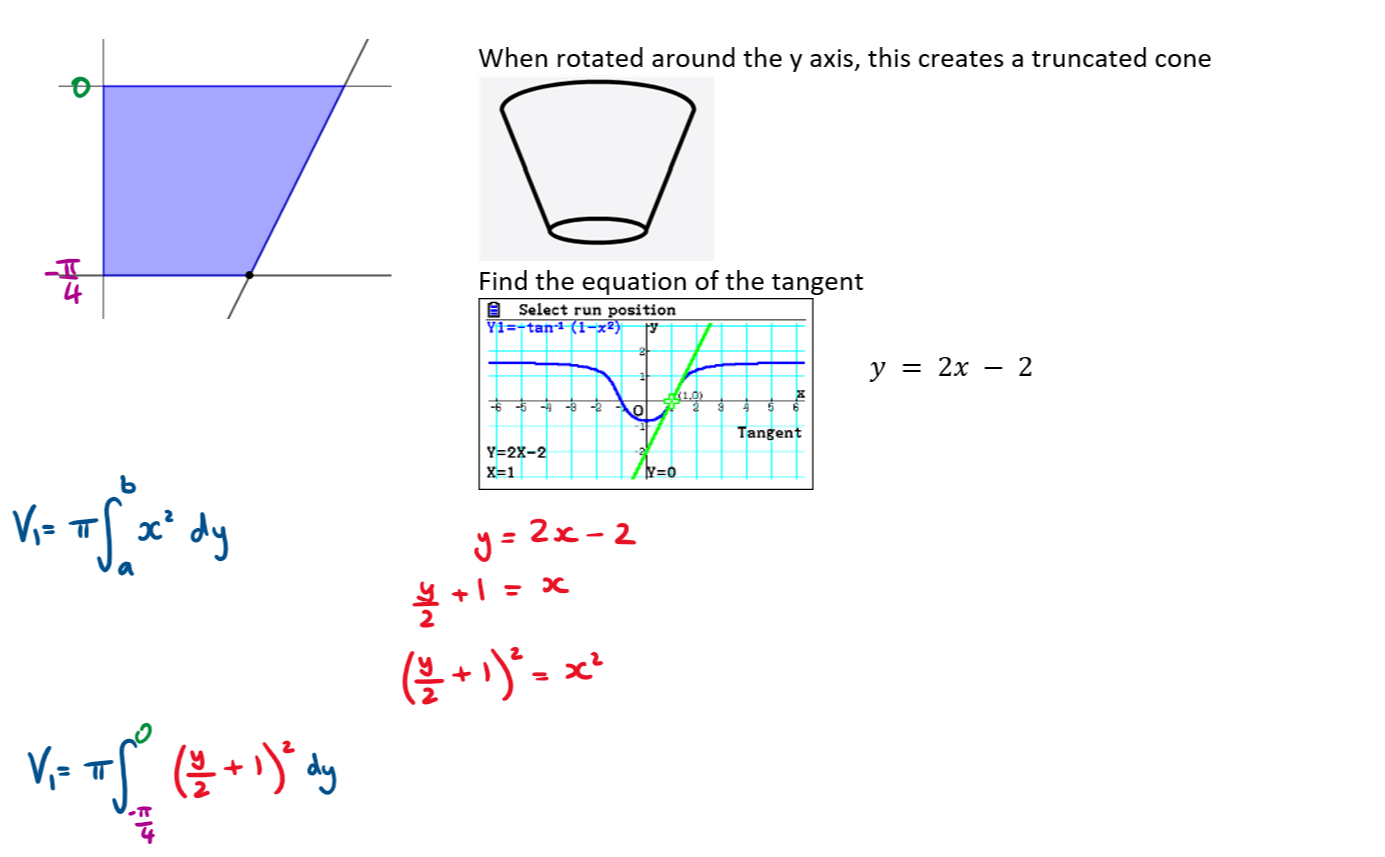
The graph shows \(\large f(x) = -\arctan(1-x^2)\), the tangent to the curve at (1 , 0) and the tangent to the curve at the point \(\large(-\frac{\pi}{4},0)\).
The shaded region is bounded by the curve and the two tangents. This region is rotated \(\large 2\pi\) around the y axis to forma solid.
Find the volume of this solid correct to 3 significant figures.
Hint
You can use your calculator for this question.
Ensure that your calculator is in radian mode.
Full Solution



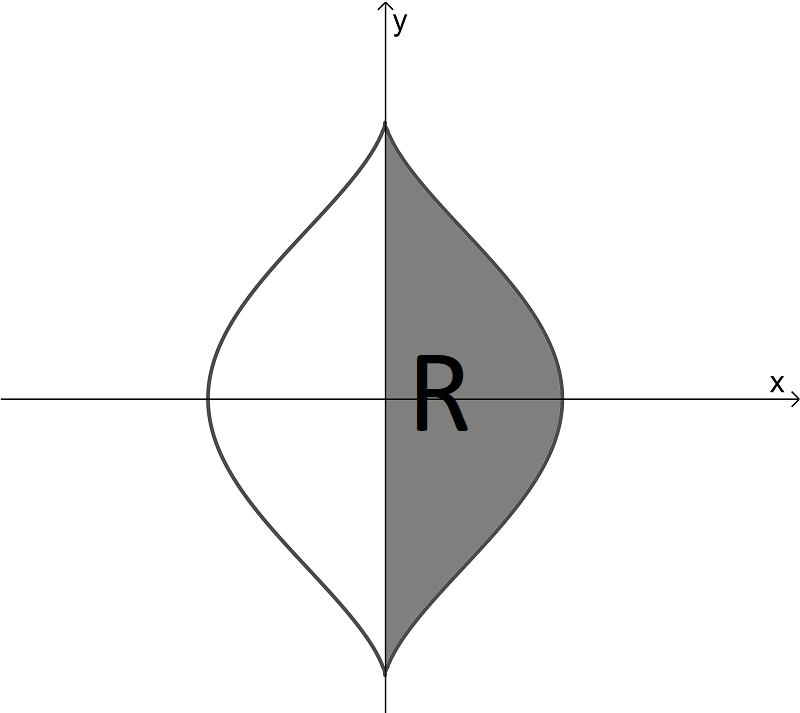
The following diagram shows the graph of \(\large x^2=\cos^3y\) for \(\large -\frac{\pi}{2}\le y\le\frac{\pi}{2}\)
The shaded region R is the area bounded by the curve, the y axis and the lines \(\large y=-\frac{\pi}{2}\) and \(\large y=\frac{\pi}{2}\).
The rgion is rotated about the y axis through \(\large 2\pi\) to form a solid.
Show that the volume of the solid is \(\large \frac{4\pi}{3}\)
Hint
To perfom the integration, write
\(\large \cos^3y=\cos y\cdot\cos^2y=\cos y\ (1-\sin^2y)\)
Full Solution
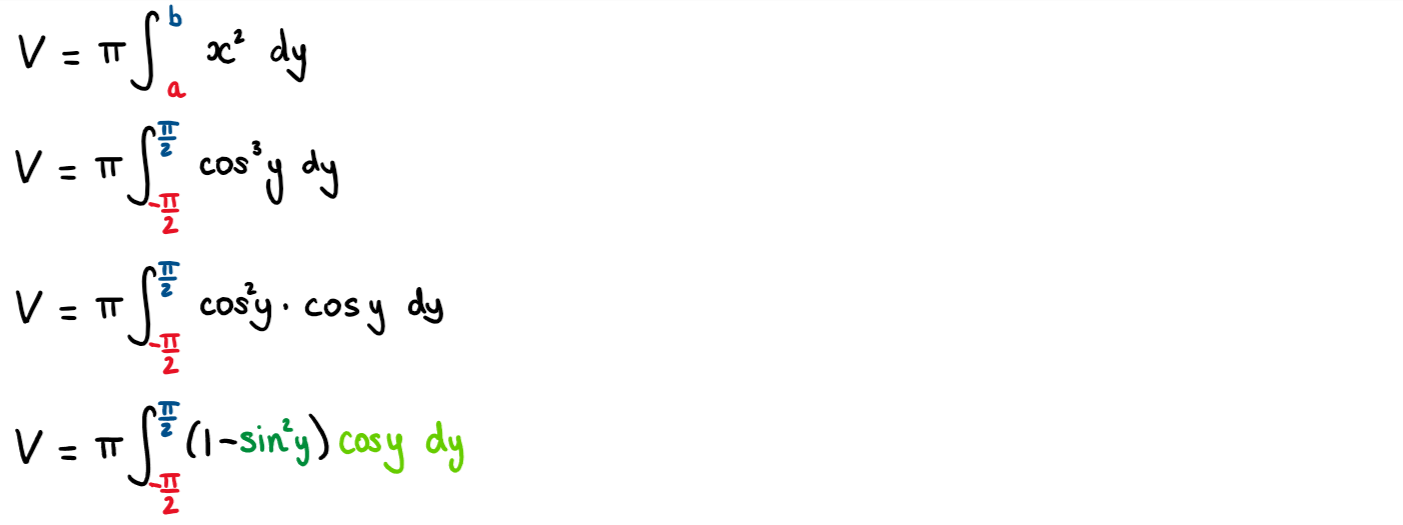


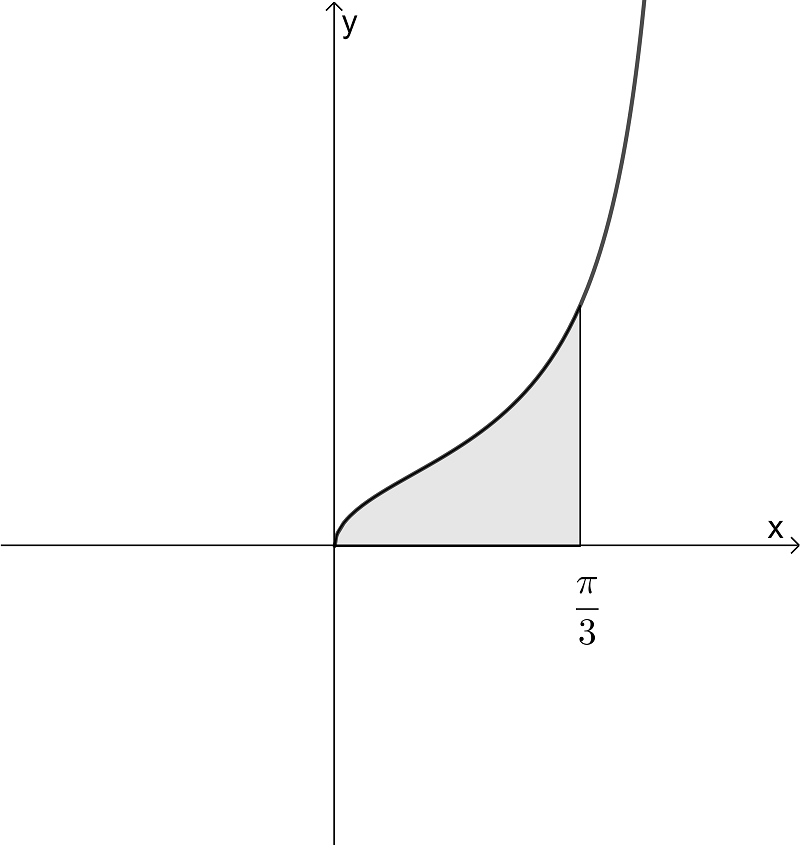
The following diagram shows the graph of the function \(\large f(x)=\frac{\sqrt{x}}{\cos x}\) for \(\large 0\le x \le\frac{\pi}{2}\)
The shaded region is the area bounded by f, the x axis, x= 0 and x = \(\large \frac{\pi}{3}\)
The region is rotated about the x axis through \(\large 2\pi\) to form a solid.
Find the volume of the solid.
Hint
It is the integration that makes this question difficult.
For the integration by substitution, let
\(\large u=x \qquad \frac{dv}{dx}=\sec^2x\)
Full Solution
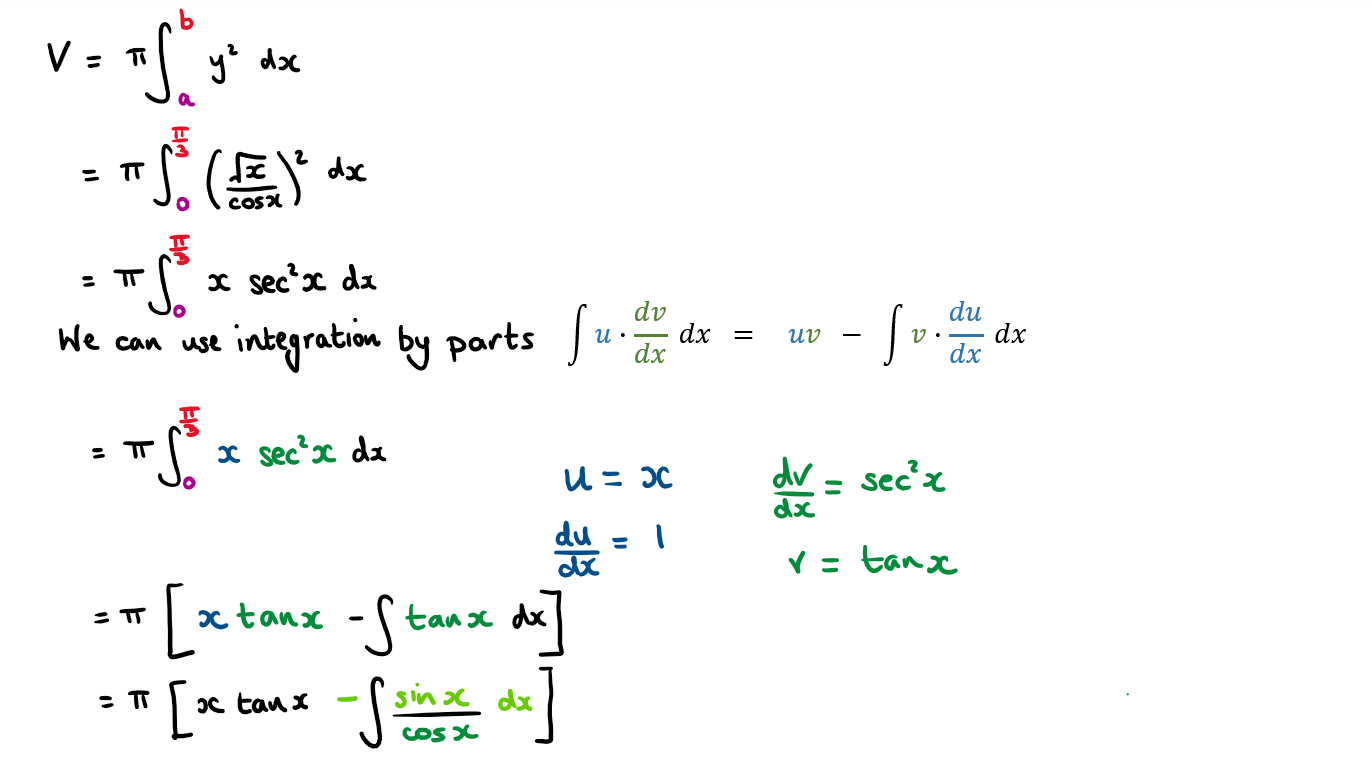

Let \(\large f(x)=\frac{-x-7}{x^2-x-6} \quad ,x\neq-2,x\neq3\)
a) Express f(x) in partial fractions
b) Hence, find the exact value of \(\large \int_{-1}^2f(x)dx\) giving your answer in the form \(\large lnq \quad,q\in\mathbb{Q}\)
Hint
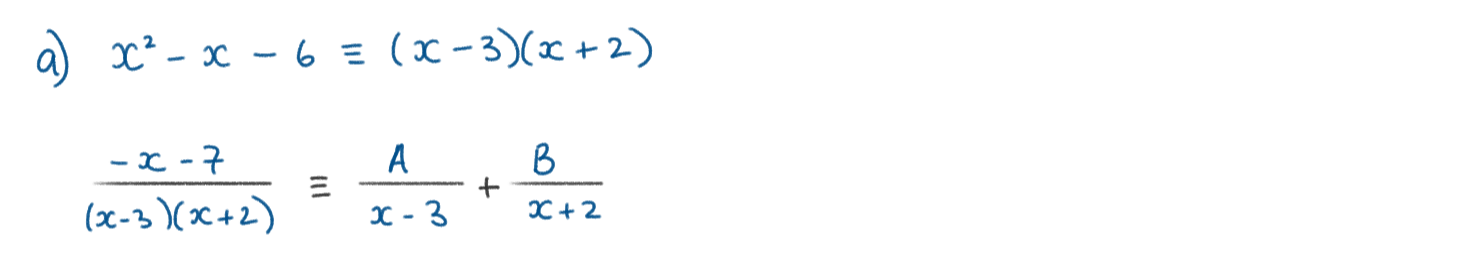
Full Solution
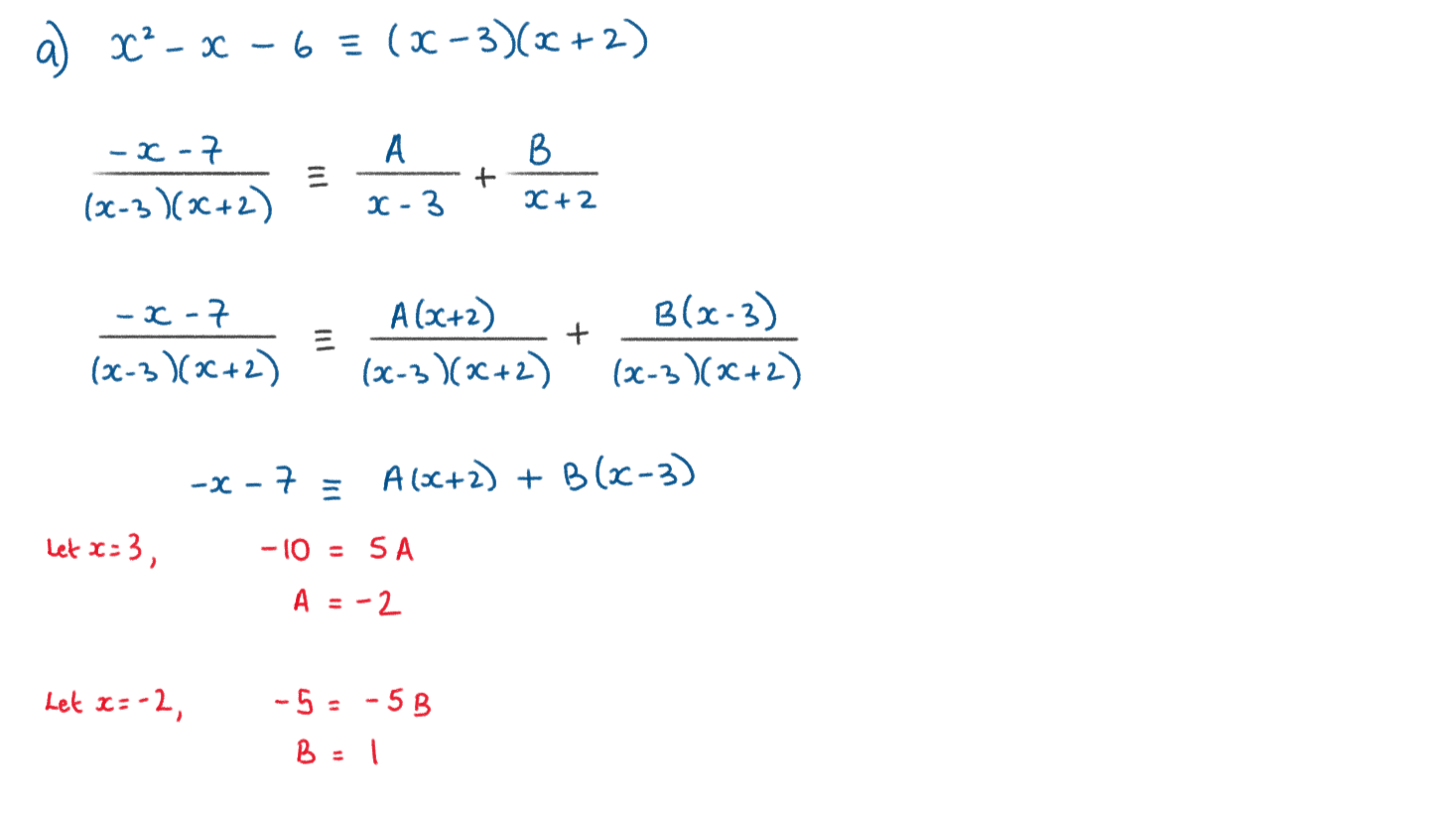

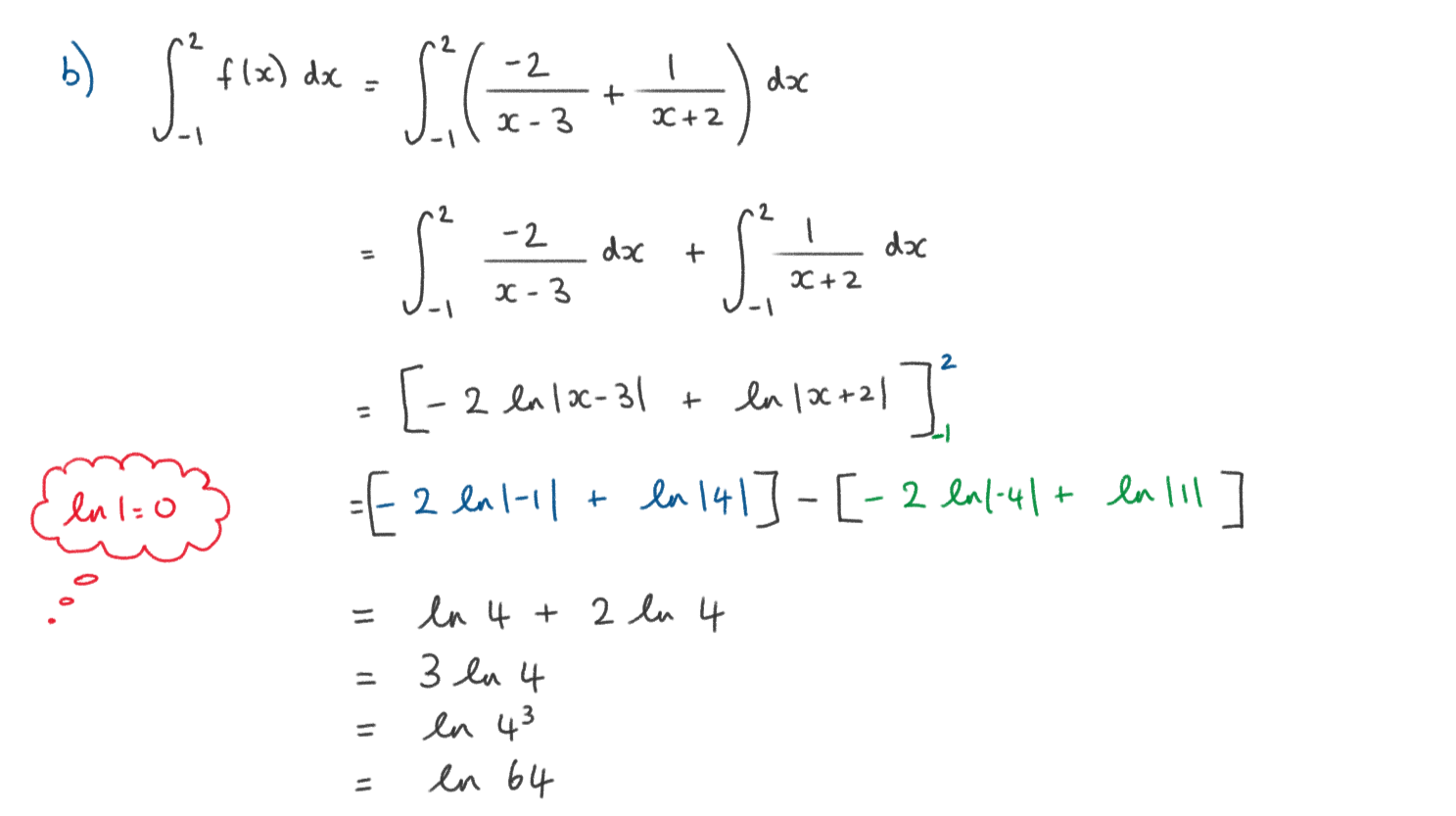

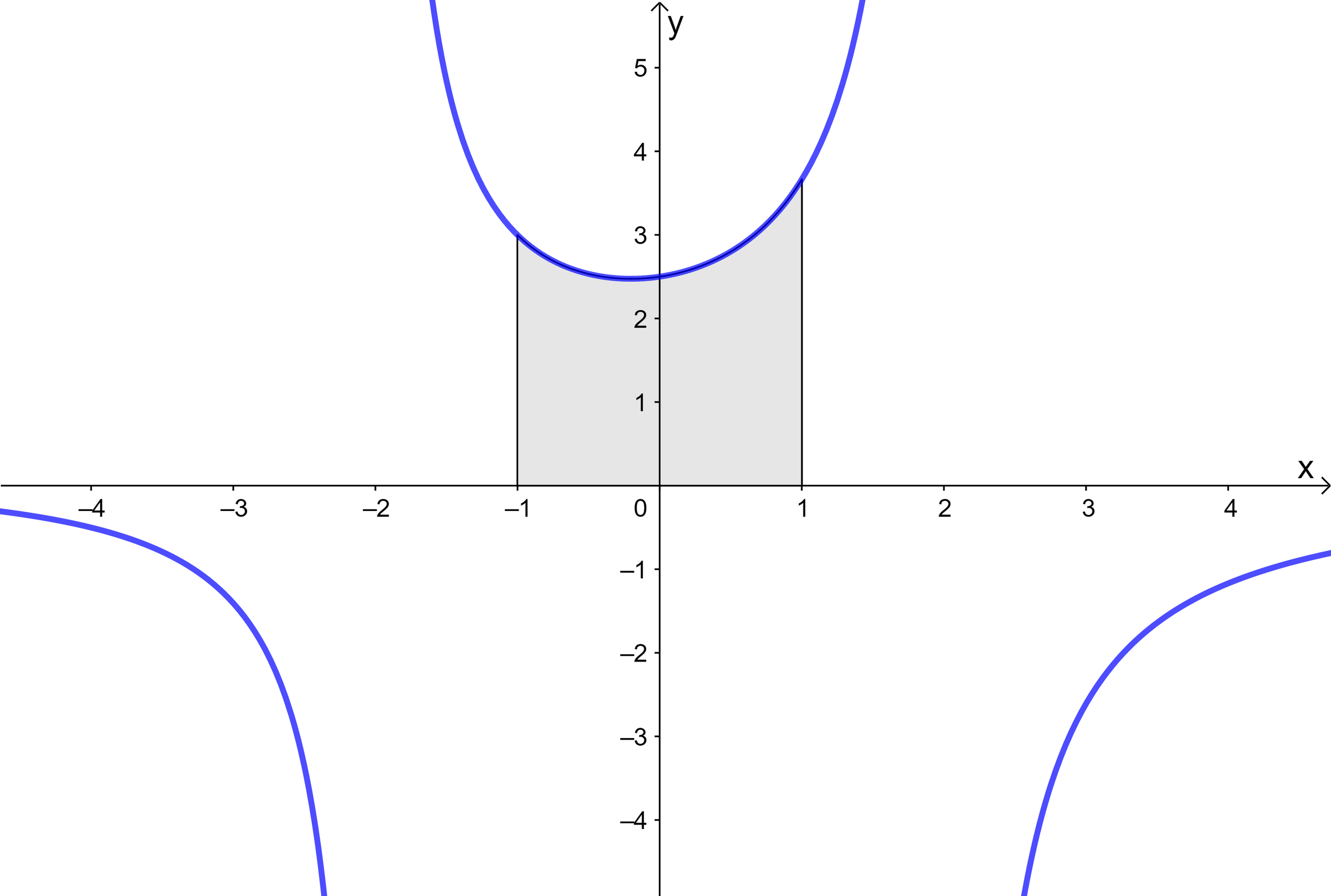
The graph shows the function \(\large f(x)=\frac{x+10}{4-x^2} \quad ,x\neq-2,x\neq2\)
By writing f(x) as the sum of two partial fractions, show that the area bounded by the curve, the x axis and the lines x = -1 and x = 1 is equal to \(\large 5ln3\)
Hint
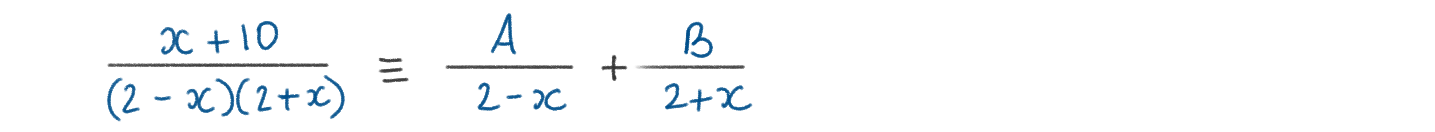
Full Solution
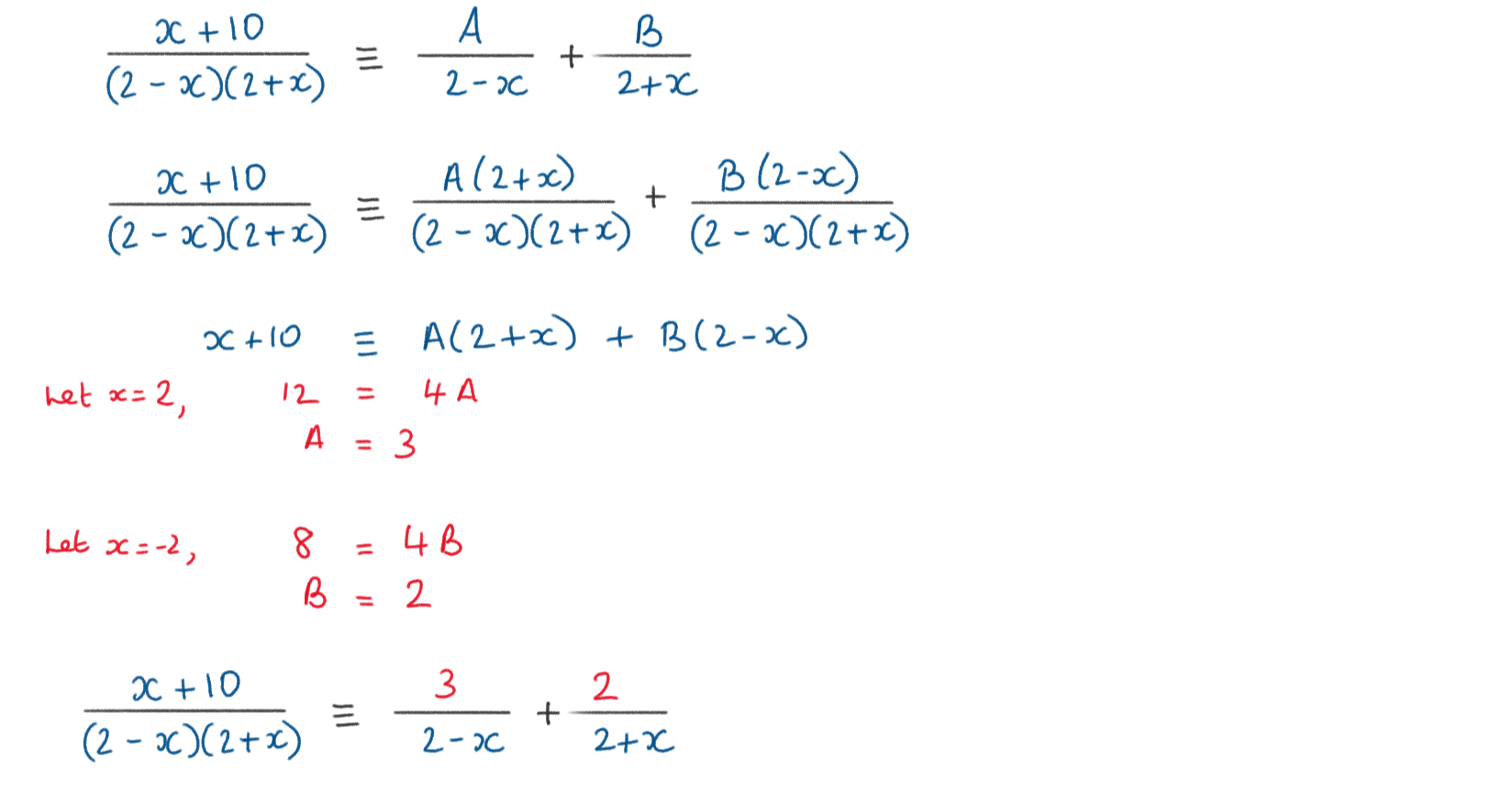
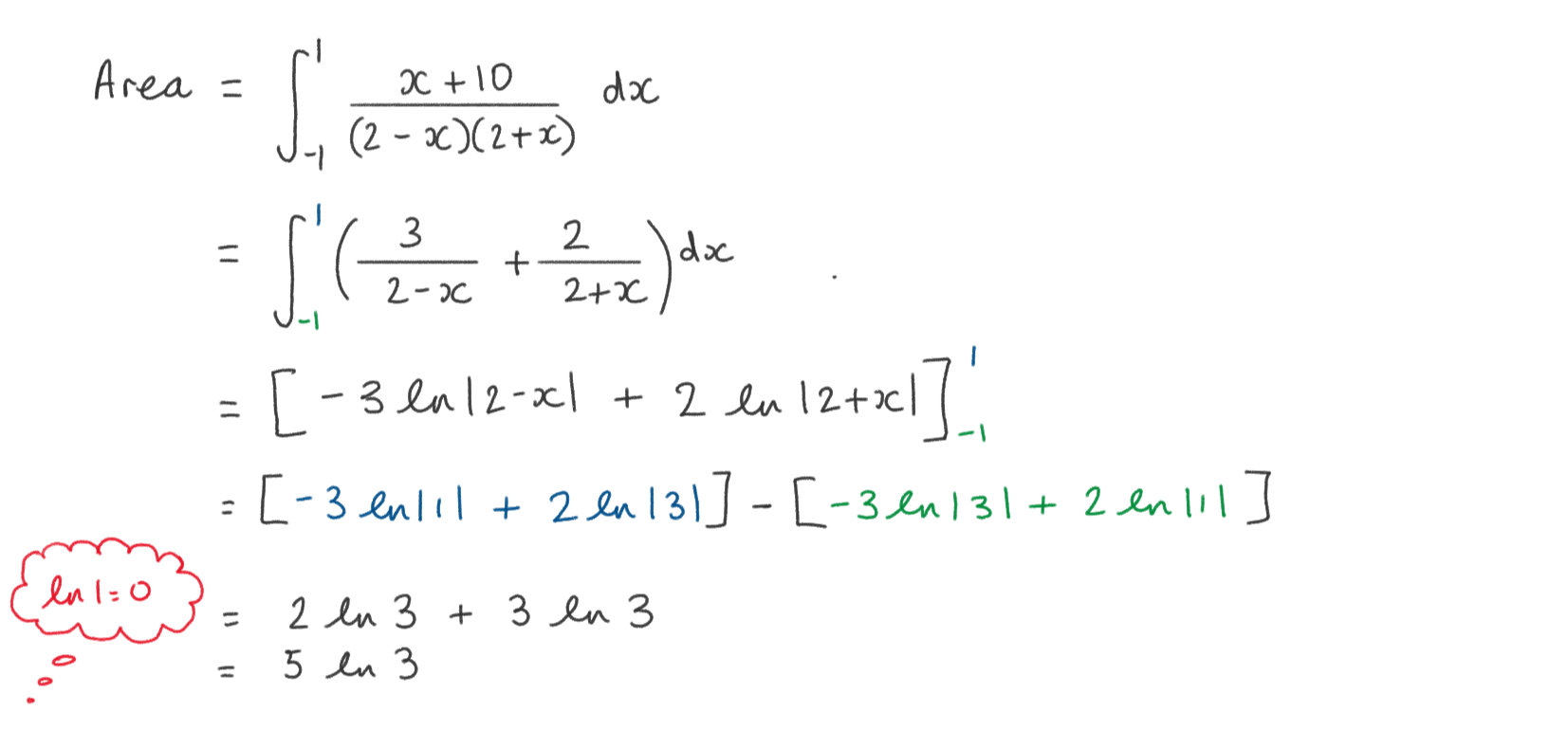


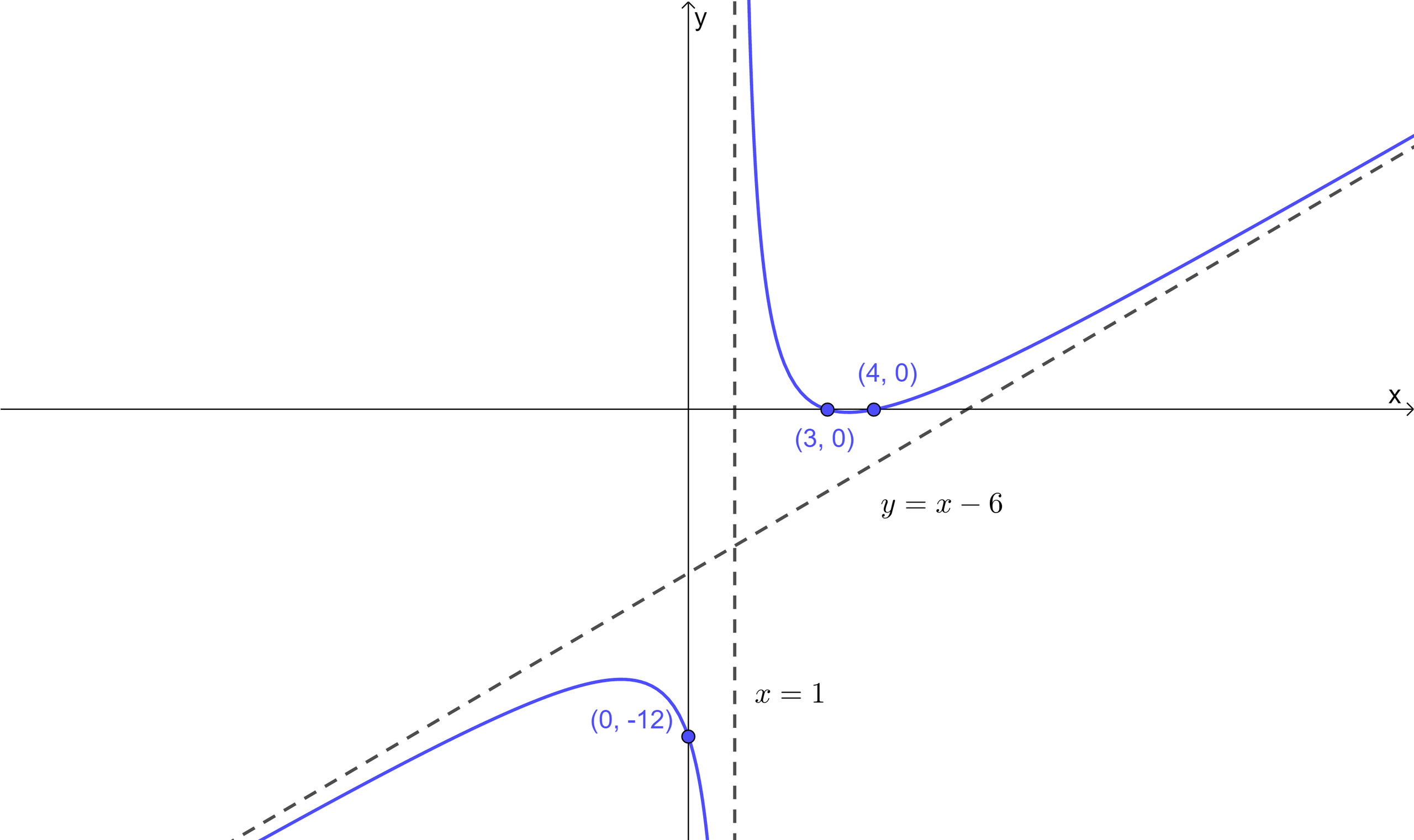
Consider the finction \(\large f(x)=\frac{x^2-7x+12}{x-1} \quad ,x\neq1\)
Find the coordinates where the graph of f crosses the
a i) x axis
ii) y axis
b) Write down the equation of the vertical asymptote of f
c) Write down the equation of the oblique asymptote of f
d) Sketch the graph of f for \(\large -15\le x \le15\) clearly indicating the points of intersection with each axis and any asymptotes
e) Express \(\large \frac{1}{f(x)}\) in partial fractions
f) Hence, find the exact value of \(\large \int_1^2\frac{1}{f(x)}dx\) in the form \(\large lnq \quad,q\in\mathbb{Q}\)
Hint
Full Solution
a i) \(\large f(x)=\frac{x^2-7x+12}{x-1} \quad ,x\neq1\)
x intercepts when f(x) = 0
\(\large \frac{x^2-7x+12}{x-1}=0\\ \large {x^2-7x+12}=0\\ \large (x-3)(x-4)=0\\ \large x = 3, \quad x = 4\)
a ii) y intercepts when x = 0
\(\large f(0)=\frac{12}{-1} =-12\)
b) \(\large f(x)=\frac{x^2-7x+12}{x-1} \quad ,x\neq1\)
Vertical asymptote when \(\large x - 1 = 0\\ \large x= 1\)
c) To find oblique asymptote, divide
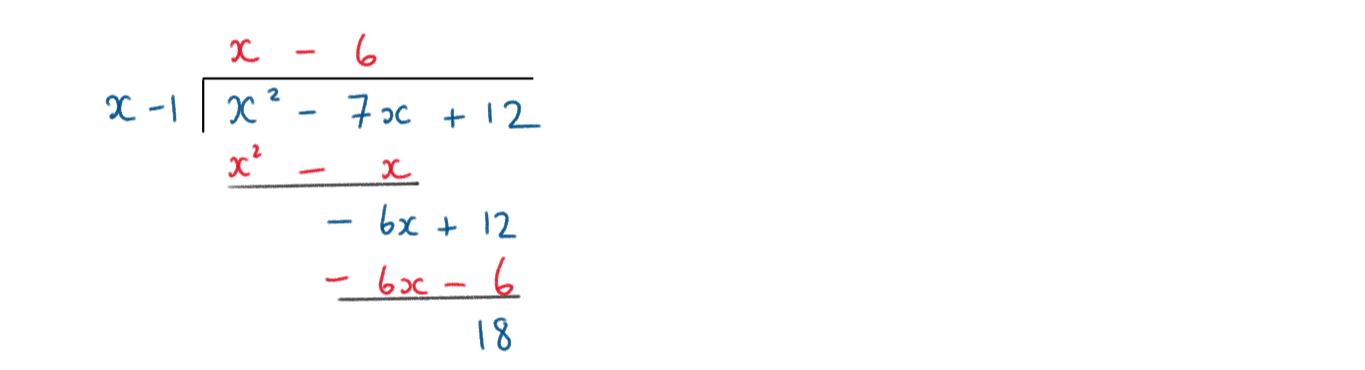
Hence, \(\large f(x)=x-6+\frac{18}{x-1}\)
Hence, oblique asymptote at y = x - 6
d)
e) \(\large \frac{1}{f(x)}=\frac{x-1}{x^2-7x+12} \quad ,x\neq3, x\neq4\)
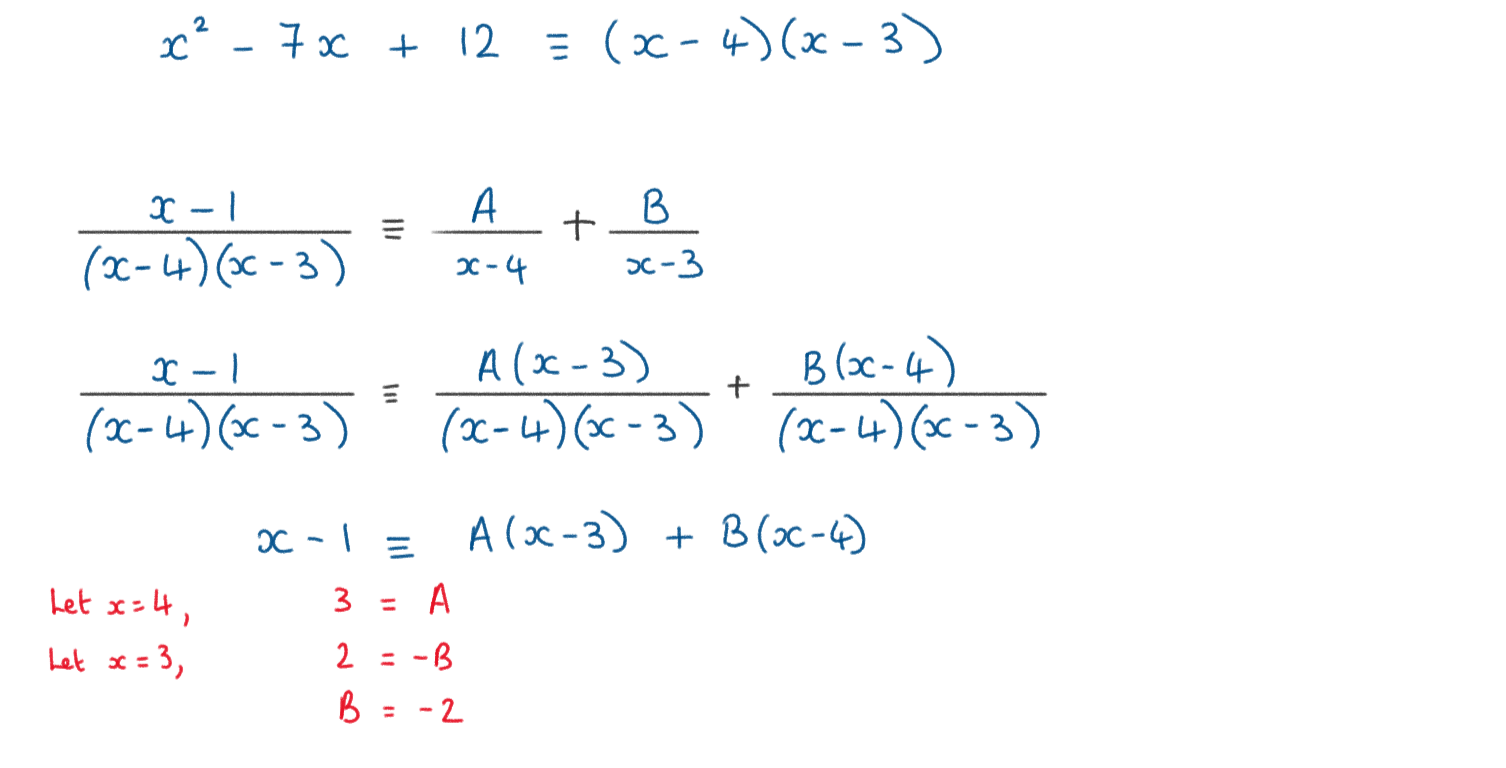
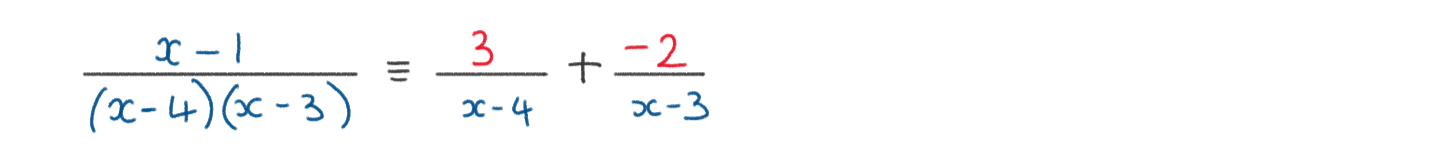
f)
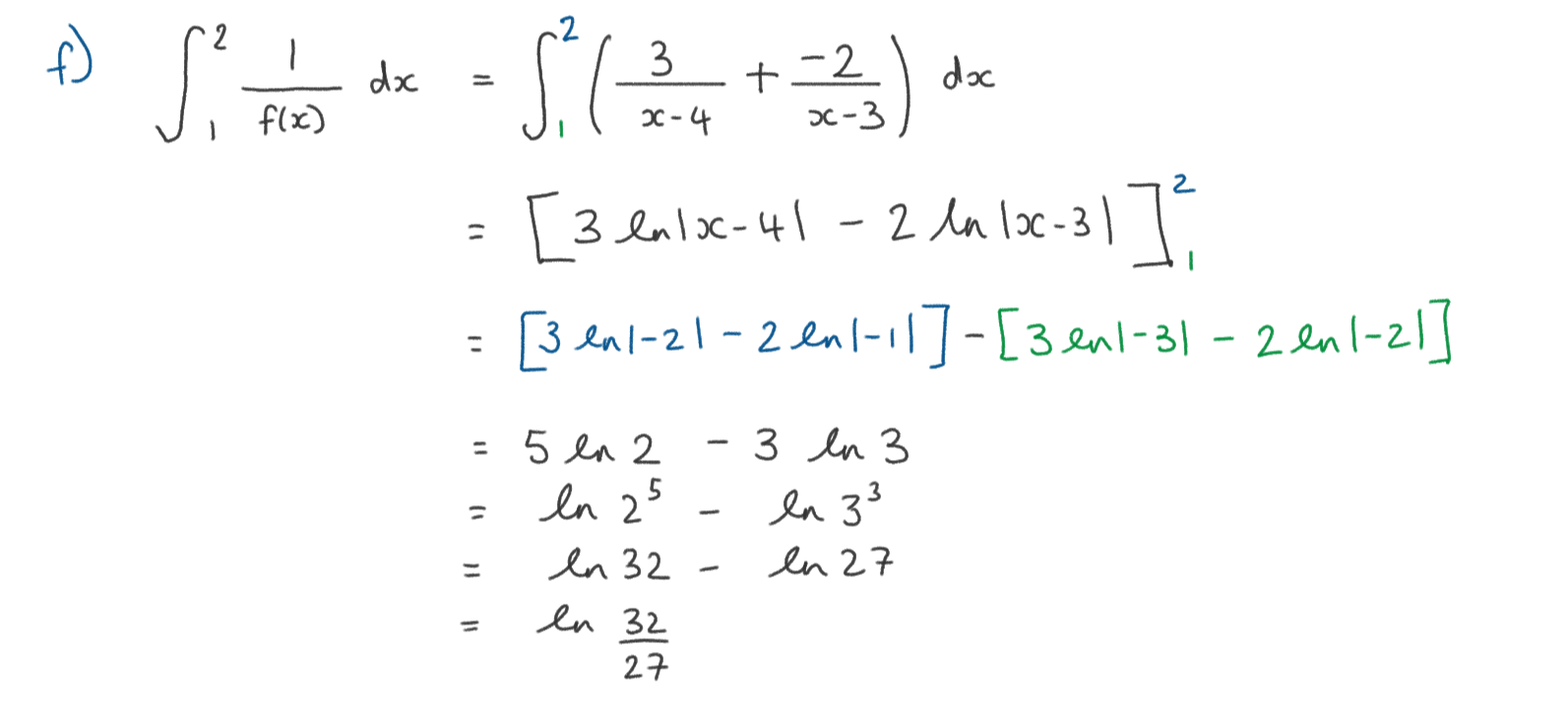


a) Find \(\int { \frac { { e }^{ x } }{ 1+{ e }^{ x } } dx } \)
b) Evaluate \(\int _{ \frac { { \pi }^{ 2 } }{ 4 } }^{ \pi ^{ 2 } }{ \frac { cos\sqrt { x } }{ \sqrt { x } } } dx\)
Hint
a) This question requires us to use integration by substitution (or recognition)
u =1 + ex
b) This question requires us to use integration by substitution
u = \(\sqrt{x}\)
Full Solution
Print from here
 Video Solution
Video Solution



Let R be the region bounded by f, the x-axis, x = 1 and x = 2
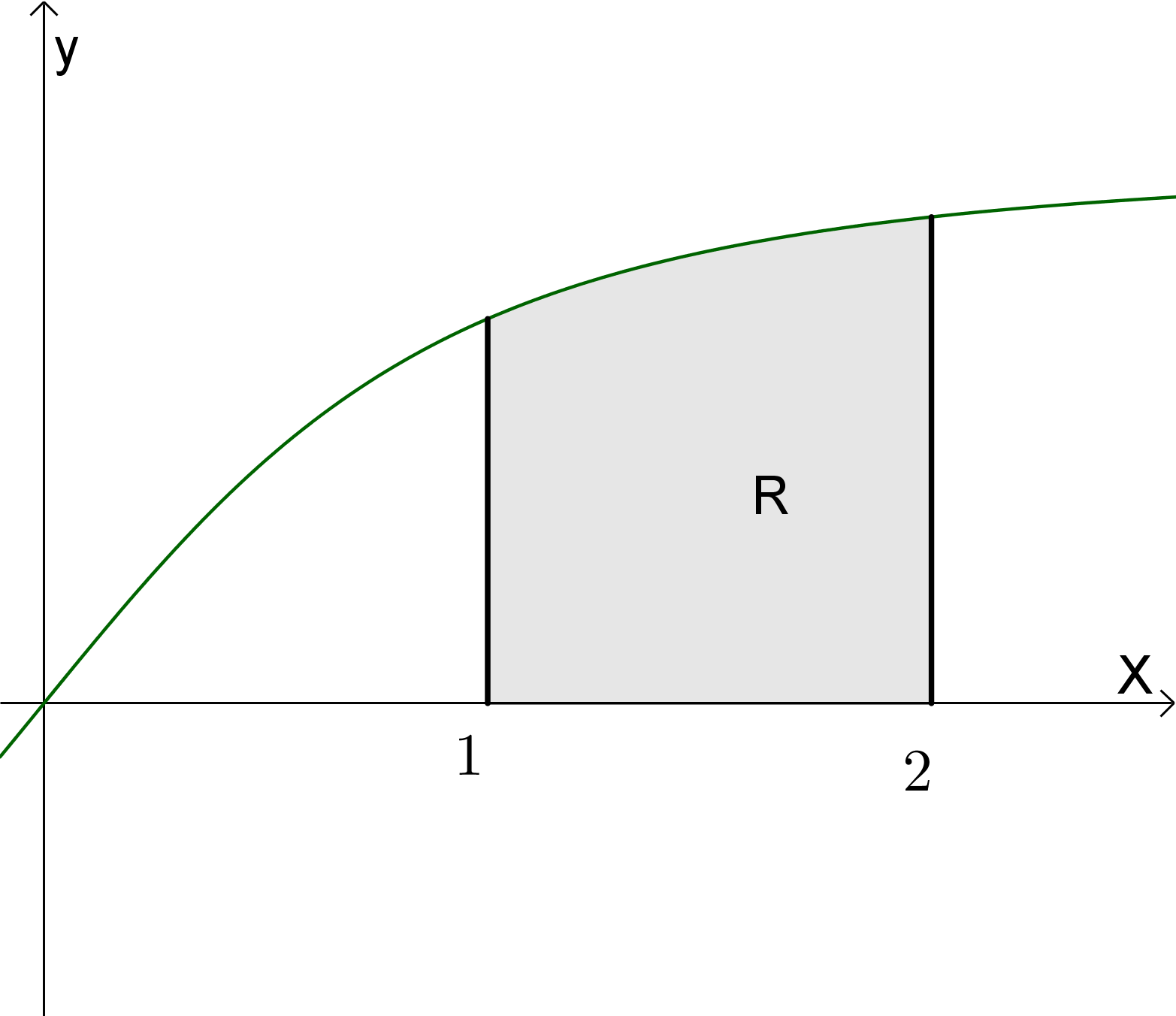
Find R
Hint
This question requires you to how to find the area under the graph: Area = \(\int _{ a }^{ b }{ y }\ dx\)
The integral requires integration by substitution
u = x2 +1
Full Solution
Print from here
 Video Solution
Video Solution


a) Using the fact that \(tanx = \frac{sinx}{cosx} \), show that \(\frac{d}{dx}(tanx) = \frac{1}{cos^2x}\)
b) Hence, find \(\int { \frac { \sqrt { tanx } }{ cos^{ 2 }x } } dx\)
Hint
a) This requires you to use the Quotient Rule
b) Hence means that you should use the result from part a)
Use Integration by substitution u = tanx
Full Solution
Print from here
 Video Solution
Video Solution


Hint
To complete this question, we need to split the integral into two parts
\(\int { \frac { arcsinx+x }{ \sqrt { 1-x^{ 2 } } } } dx=\int { \frac { arcsinx }{ \sqrt { 1-x^{ 2 } } } } dx+\int { \frac { x }{ \sqrt { 1-x^{ 2 } } } } dx\)
Both these integrals can be completed using Integration by substitution
Full Solution
Print from here
 Video Solution
Video Solution


Hint
This might help
\(sin^5x = sin^4x\cdot sinx = (sin^2x)^2\cdot sinx\)
You will need to use Integration by substitution
Can you think of a substitution that will work?
Full Solution
Print from here
 Video Solution
Video Solution


Hint
This is a tricky question that requires very careful manipulation
The substitution gives \(\frac{dx}{d\theta}=\frac{4}{3}cos\theta\)
The integral becomes \(\int { \sqrt { 16-16sin^{ 2 }\theta } \cdot \frac { 4 }{ 3 } cos\theta \quad d\theta } \)
Full Solution
Print from here
 Video Solution
Video Solution


Hint
You need to use the method of integration by parts
You should apply the method twice and the integral to find should be a multiple of the question
Full Solution
Print from here
 Video Solution
Video Solution


Hint
The solution requires you to use Integration by Parts
Think of the question as \(\int { 1\cdot arctanxdx } \)
Full Solution
Print from here
 Video Solution
Video Solution


Hint
This question requires you to use Integration by Parts
In the second part you will need to integrate a rational function. Since the degree of the numerator is equal to the degree of the denominator, you need to divide the polynomials
Full Solution
Print from here
 Video Solution
Video Solution

Solve the differential equation given that y(0) = 2
\({\large \frac{dy}{dx}=\frac{e^x}{y}, \quad y>0}\)
Hint
This is a separable differential equation.
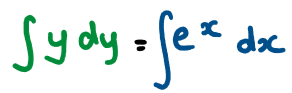
Full Solution
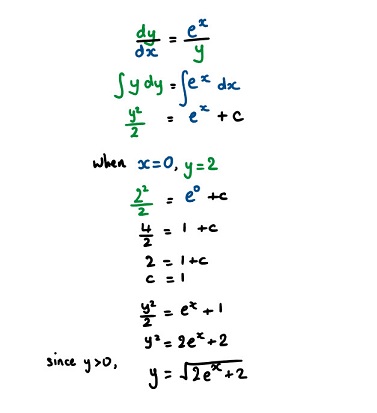
a) Write \({\huge \frac{1}{4-x^2}}\)as the sum of two partial fractions
b) Hence, given that y(0) = 0, find the particular solution of the differential equation in the form
Hint
b) This is a separable differential equation
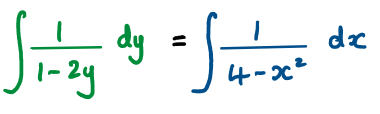
Use the result from part a) to re-write the second integrand
Full Solution
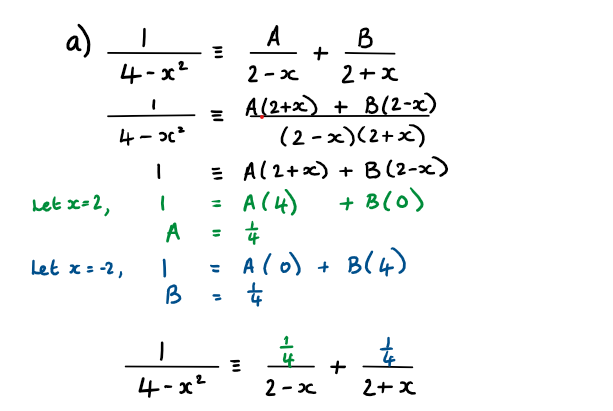
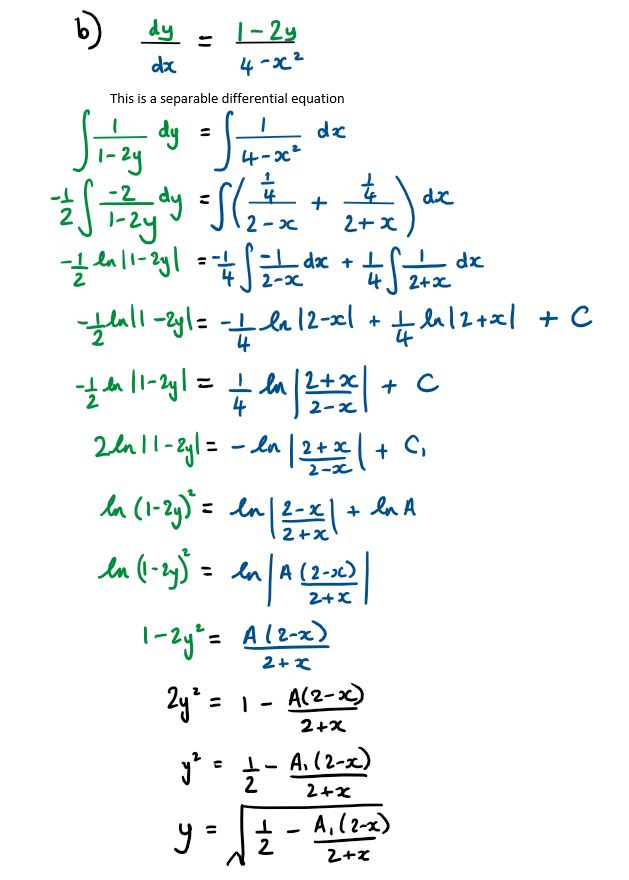

a) Express \(\frac{3}{x(x-3)}\) as the sum of two partial fractions
The population of a species of fish can be modelled by the differential equation \(\large \frac{\text{d}N}{\text{d}t}=\frac{2}{3}N(N-3)cos2t\)
where N = population in thousands, t = time in years
b) Given that initially the population of fish is 4000, show that \(\large N=\frac{12}{4-e^{sin{2t}}}\)
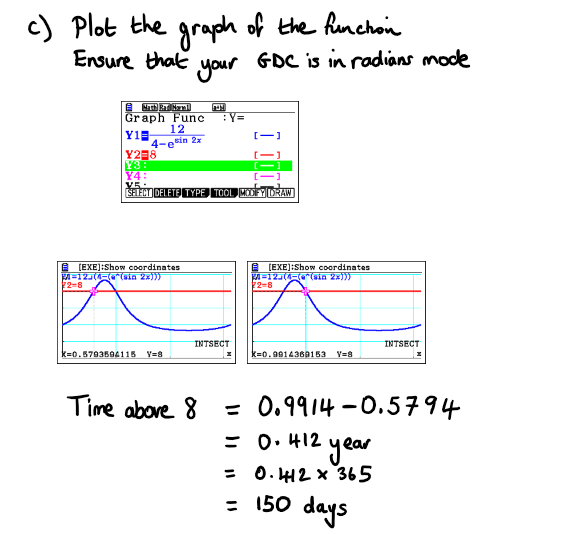
c) How many days during the first year is the population of fish above 8000?
Hint
a) Work out \(\large \frac{3}{x(x-3)}\equiv\frac{A}{x}+\frac{B}{x-3}\)
b) This is a variables separable differential equation
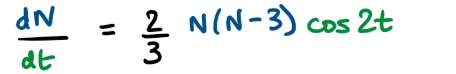
Solve for N = 4 , t = 0
c) Use your graphical calculator to find two values in the first year where N > 8
Full Solution
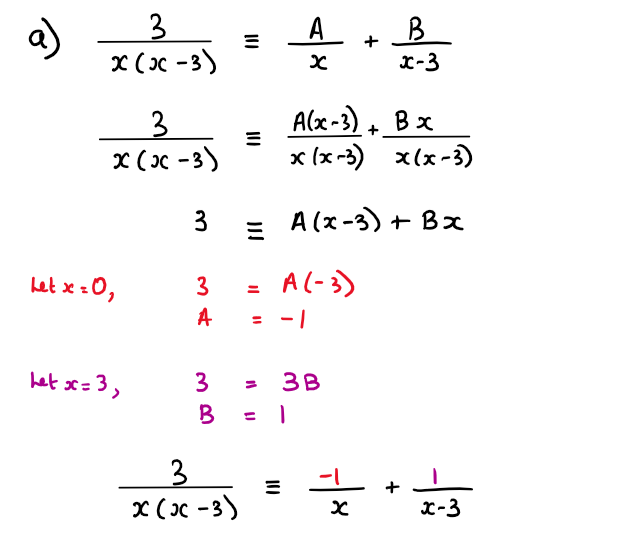

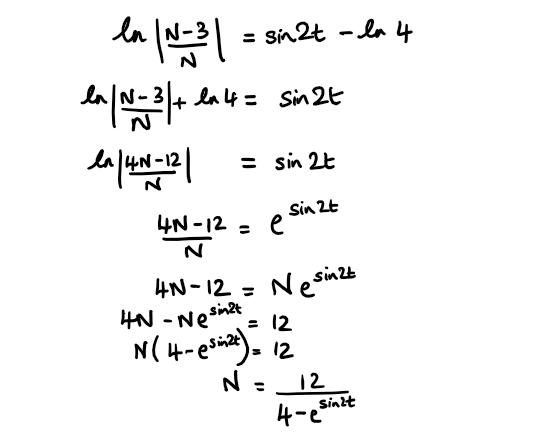

Consider the following first order differential equation
\(\large x\frac{\text{d}y}{\text{d}x}+3y=\frac{lnx}{x}\)
a) Show that x3 is the integrating factor for this differential equation
b) Hence, find the general solution of this differential equation in the form y = f(x)
Hint
b) We should recognise the product rule for differentiation 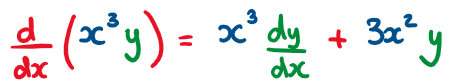
We should use integration by parts to integrate xlnx
Full Solution
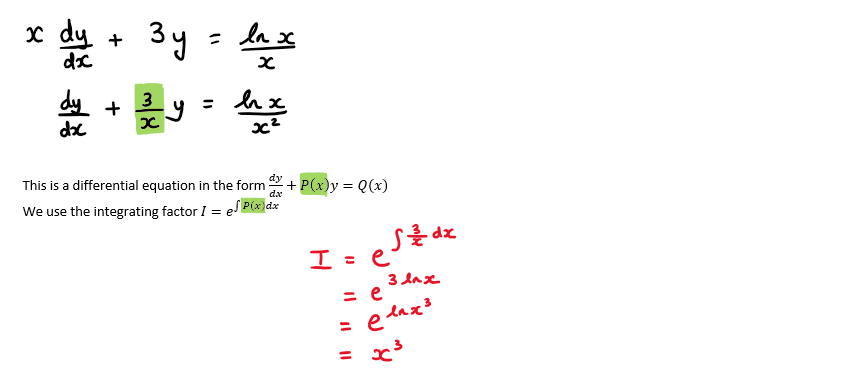


Consider the following differential equation \(\large \frac{\text{d}y}{\text{d}x}+ytanx=secx\)
a) Using a suitable integrating factor show that the differential equation can be written as \(\large \frac{y}{cosx}=\int sec^²x {dx}\)
b) Given that (0 , 2) lies on the curve, show that the particular solution of the differential equation is \(\large y=sinx+2cosx\)
Hint
a) This is a differential equation in the form \(\large \frac{\text{d}y}{\text{d}x}+P(x)y=Q(x)\)
We use the integrating factor \(I=e^{\int tanxdx }\)
We should recognise the product rule for differentiation 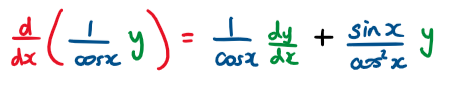
Full Solution
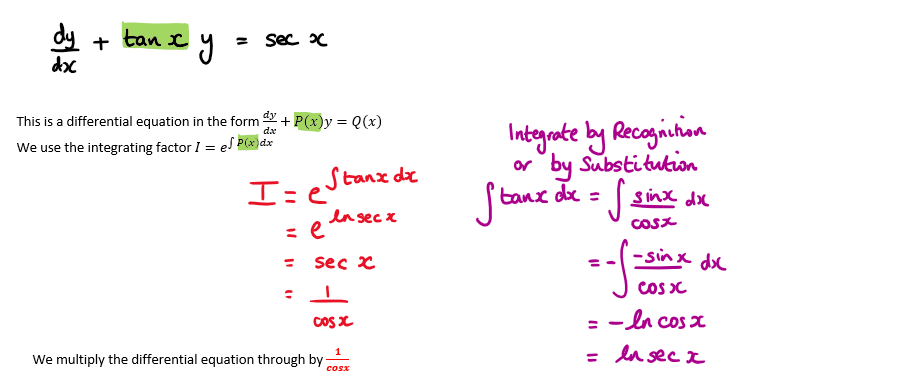
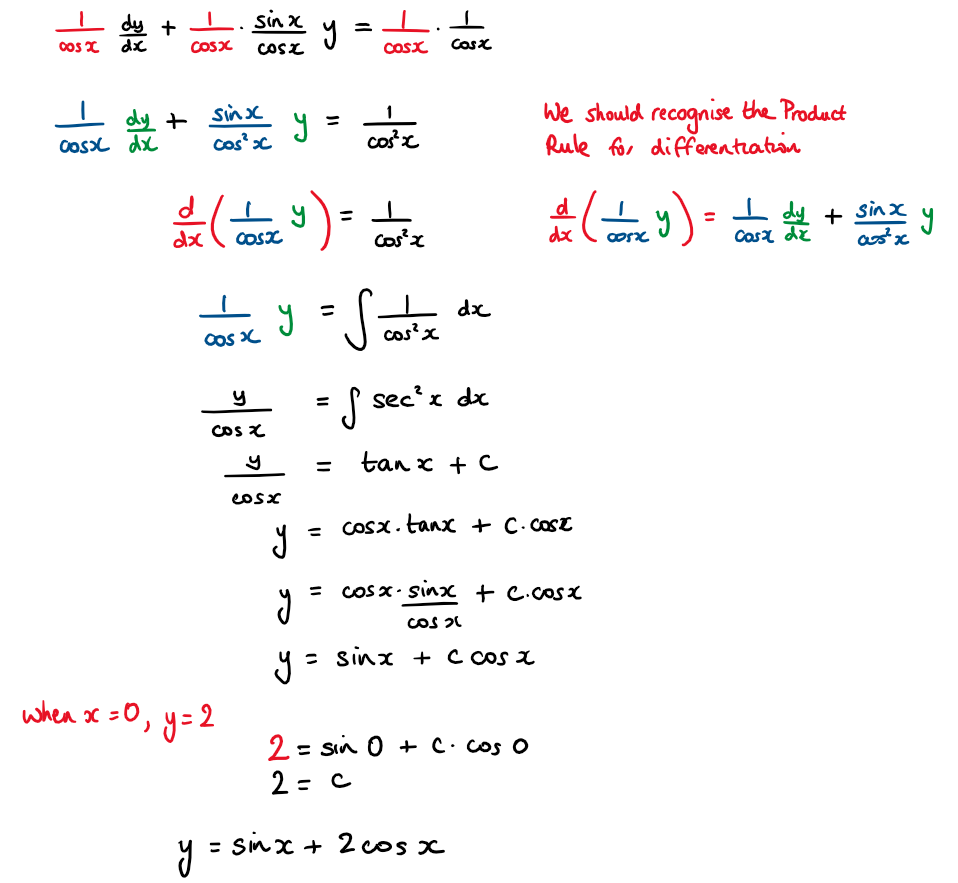

Consider the following differential equation \(\large \sin x\frac{\text{d}y}{\text{d}x}+y\cos x=2\sin^2 x\)
a) Show that the integrating factor of this differential equation is \(\large \sin x\)
b) Solve the differential equation, giving your answer in the form \(y=f(x)\)
Hint
a) This is a differential equation in the form \(\large \frac{\text{d}y}{\text{d}x}+P(x)y=Q(x)\)
We use the integrating factor \(\large I=e^{\int \frac{\cos x}{\sin x}dx }\)
b) We should recognise the product rule for differentiation 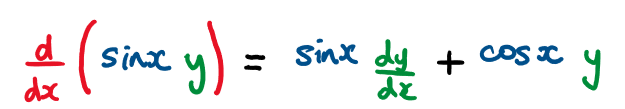
Full Solution


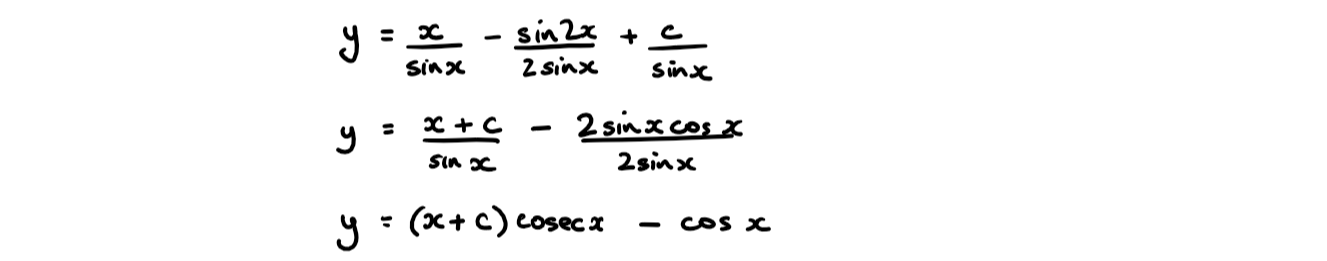

Consider the first order differential equation
\( \large xy\frac{\text{d}y}{\text{d}x}+4x^2+y^2=0 \quad,\quad y\geq0\)
a) Use the substitution y = vx to show that \( \large \frac{\text{d}v}{\text{d}x}=-\frac{4+2v^2}{vx}\)
b) Show that the solution to the differential equation for which y(1) = 0 is \(\large y=\frac{\sqrt{2-2x^4}}{x}\)
Hint
Divide both sides of the equations by x² to get in the recognisable form of a homogeneous differential equation
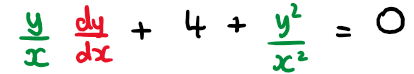
Full Solution
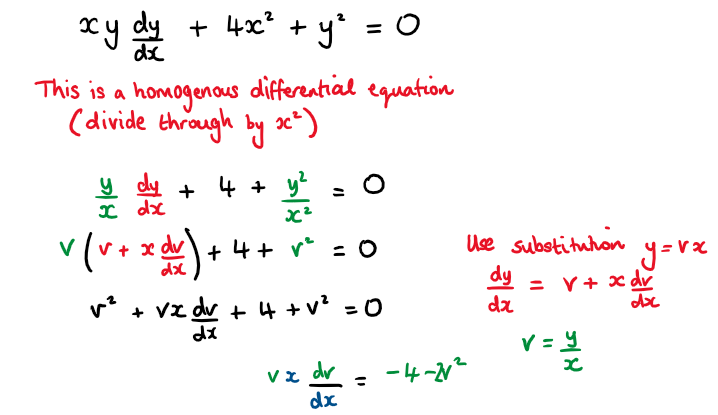
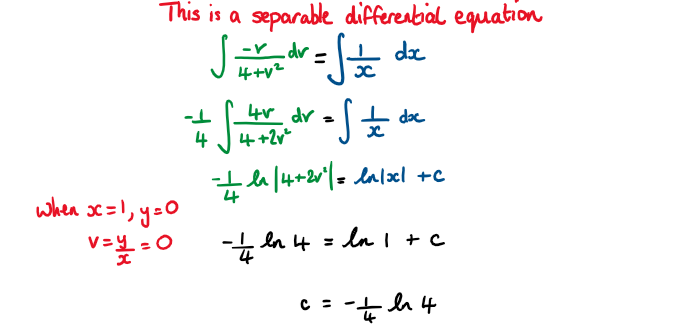
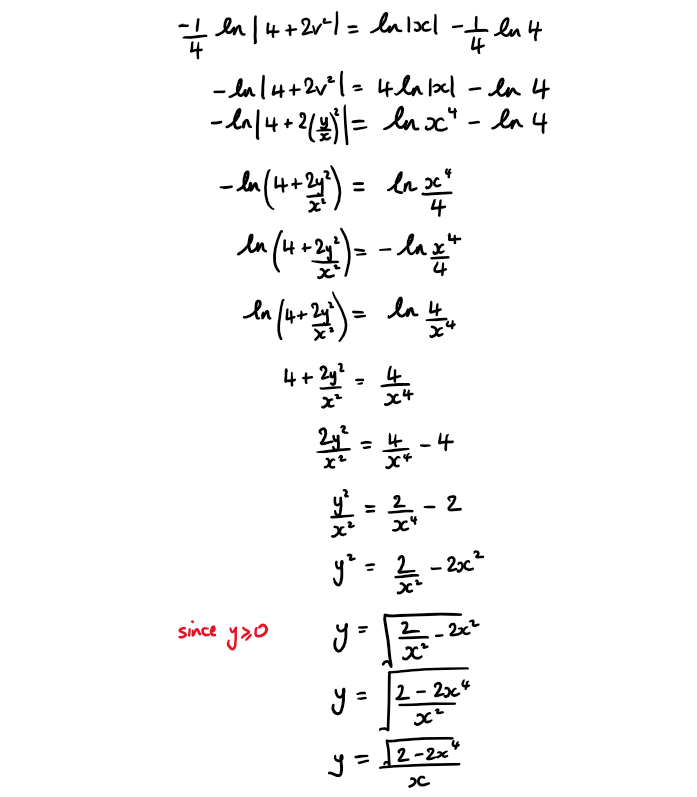

Consider the homogeneous differential equation \(\large \frac{\text{d}y}{\text{d}x}=\frac{x^2+y^2}{2xy}\)
a) Using the substitution y = vx , show that \(\large \frac{\text{d}v}{\text{d}x}=\frac{1-v^2}{2vx}\)
b) Solve the differential equation and show that y² = x² - cx
Hint
a) Divide the numerator and denominator by x² to get the differential equation in the required format to be able to substitute \(v=\frac{y}{x}\)
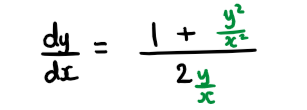
b) This is a variables separable differential equation
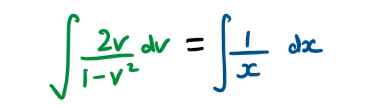
Full Solution



Consider the differential equation \(\large xy\frac{\text{d}y}{\text{d}x}=x^2\text{cosec}\frac{y}{x}+y^2\)
a) Show that this equation can be written in the form \(\large \frac{\text{d}y}{\text{d}x}=f(\frac{y}{x})\)
b) Using the substitution y = vx , show that the particular solution to the equation, given that y(1)= 0 is
Hint
a) Divide the numerator and denominator by x² to get the differential equation in the required format to be able to substitute \(v=\frac{y}{x}\)
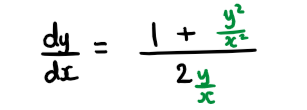
b) This is a variables separable differential equation
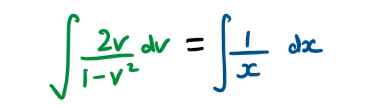
Full Solution
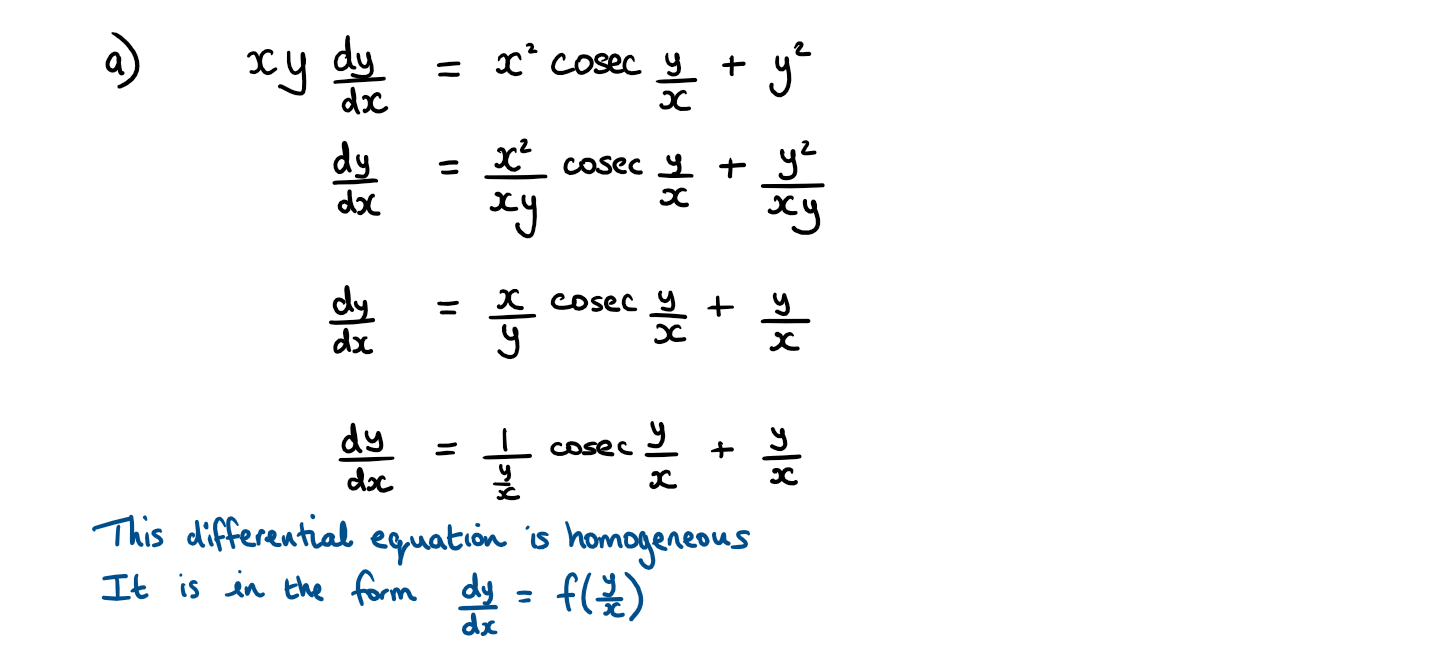
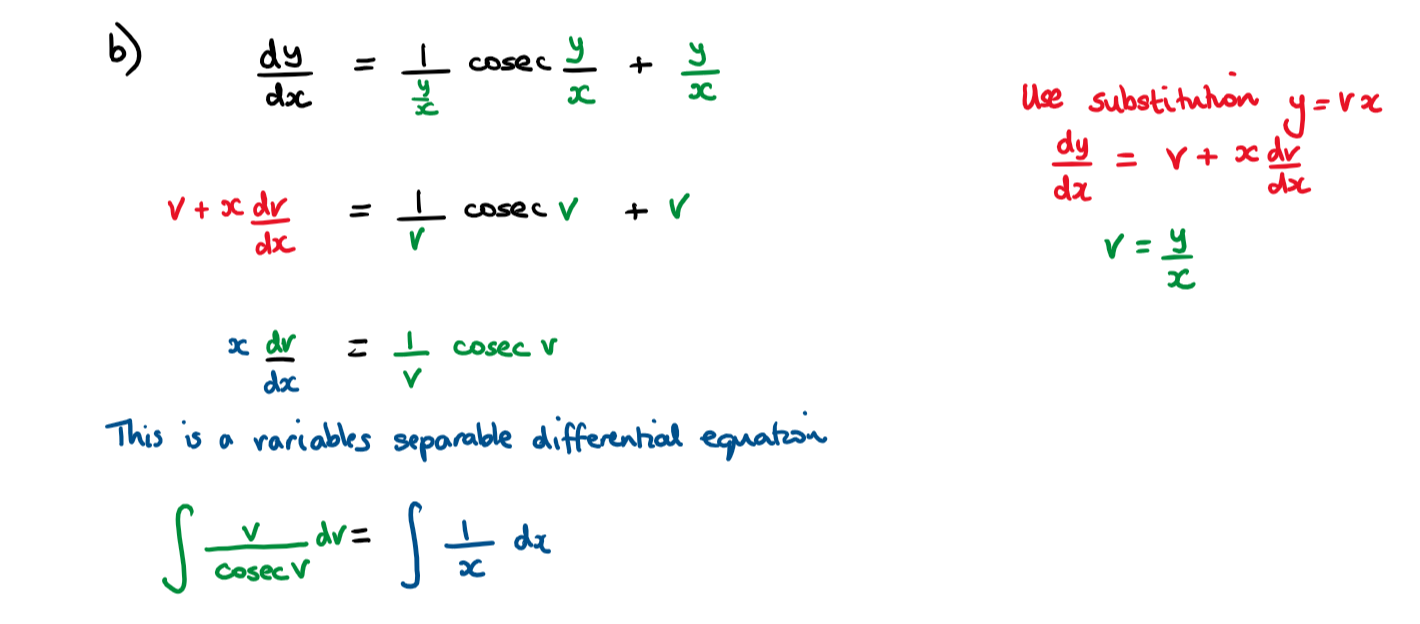
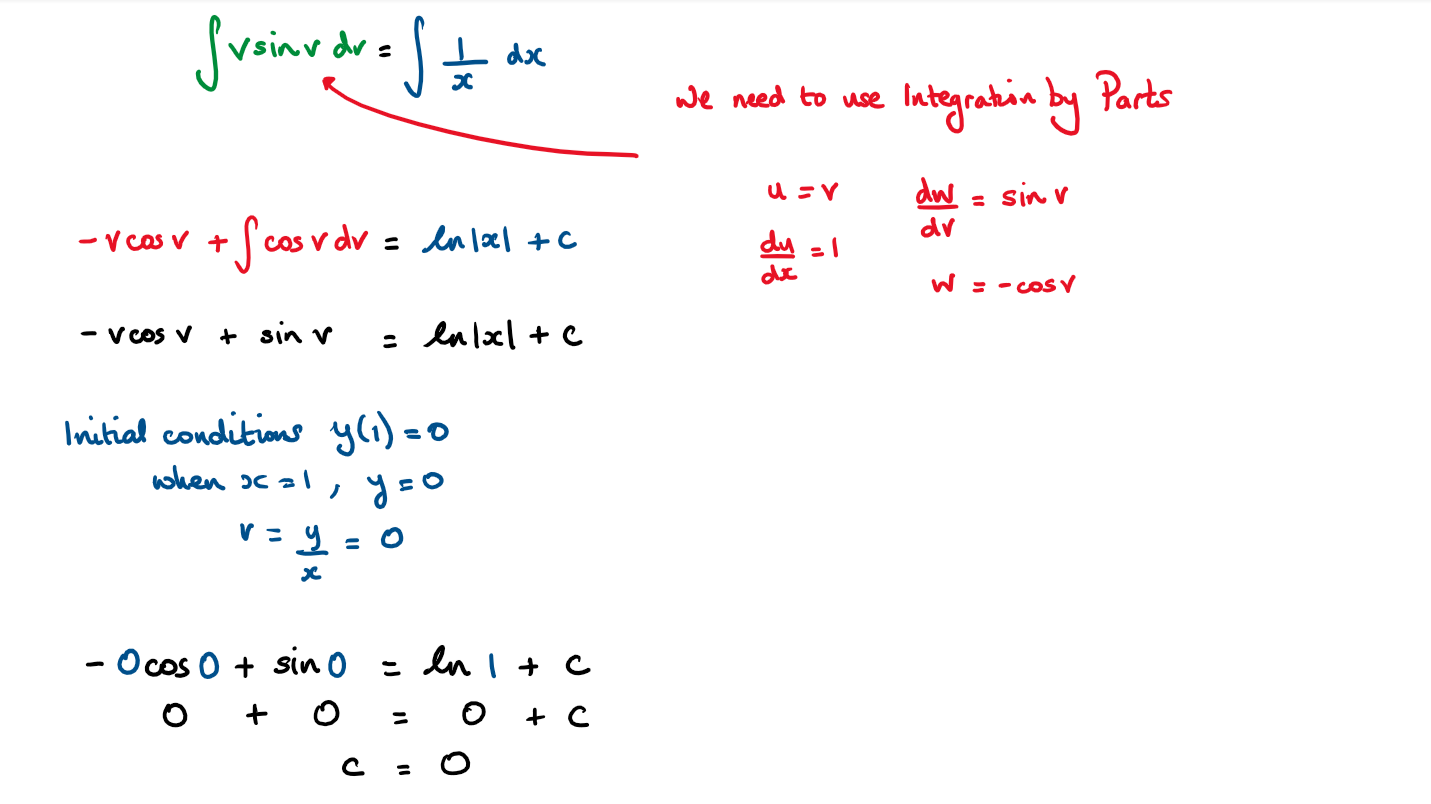
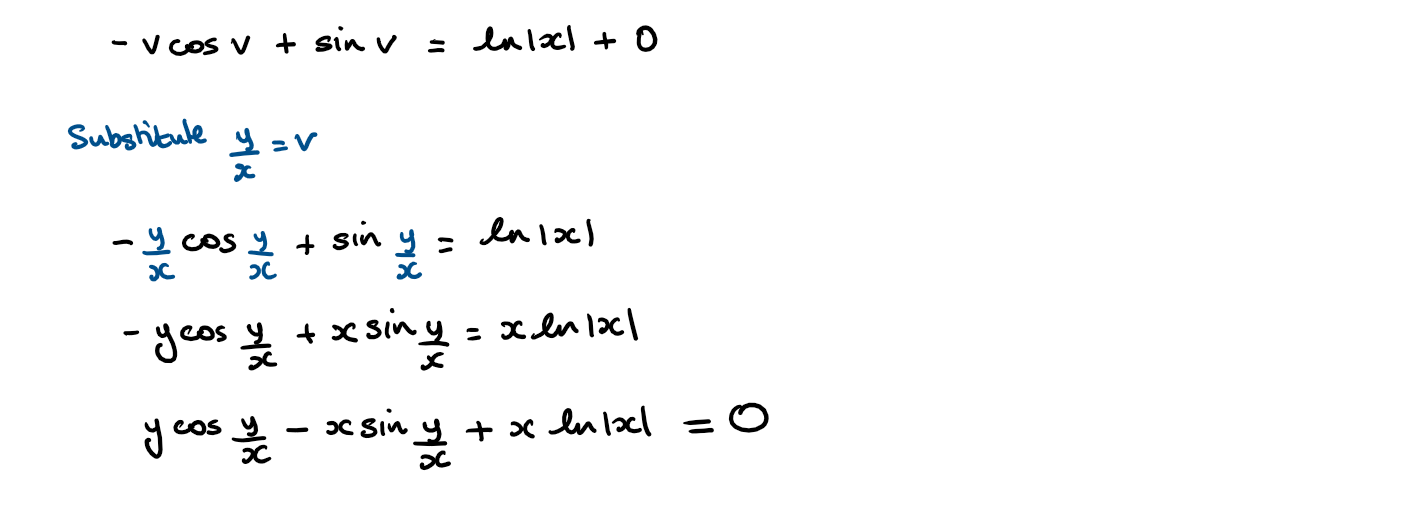
How much of Calculus Examination Questions HL have you understood?
Feedback
Which of the following best describes your feedback?



 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn