On this page you can find examination questions from the topic of statistics and probability


During week 1, a group of 60 athletes were asked to record the amount of water, X litres, that they consumed in that week. Here are the results
\(\sum x=1470\)
\(\sum x^2=36\ 132.6\)
Calculate
a. the mean of X
b. the standard deviation of X
During week 2, as part of a programme to improve their performance, the athletes were instructed to drink 10% more water. Assuming that they do this, find for week 2
c. the new mean
d. the new standard deviation
Hint
Full Solution


The world record times in seconds for the women’s 100m sprint from 1970 onwards are given below

Use your calculator to write down
a) \(\bar{x}\) , the mean year
b) \(\bar{y}\) , the mean time
c) \(r\), Pearson’s product-moment correlation coefficient
The equation of the regression line y on x is y = ax + b
d) Find the values of a and b for these data
e) Show that \((\bar{x},\bar{y})\) lies on this line
f) Use the regression line to estimate the world record time in 2024
Hint
Full Solution



Henri Tarr travels to school by bike \(\frac{3}{5}\) of the week and by car the rest of the time.
If he travels by bike, the probability that he is late is \(\frac{1}{8}\).
If he travels by car, the probability that he is late is \(\frac{3}{8}\).
a) Copy and complete the following tree diagram

b) Find the probability that Henri goes to school by car and is late for school.
c) Find the probability that he is late for school.
d) Given that he is late, find the probability that he travels to school by car.
Hint
Full Solution


 On average, it is found that 5% of AirPods* made on a production line are faulty.
On average, it is found that 5% of AirPods* made on a production line are faulty.
a) Find the probability that in a random sample of 10, there are
i) No faulty AirPods
ii) more than one faulty set of AirPods
b) A sample of n sets of AirPods is taken from the production line. If the probability that there is at least one faulty AirPod is more than 75%, find the smallest possible value of n
* Fictitious data. I’m sure that AirPods production is very reliable!
Hint
Full Solution
How much of Statistics and Probability Examination Questions HL have you understood?






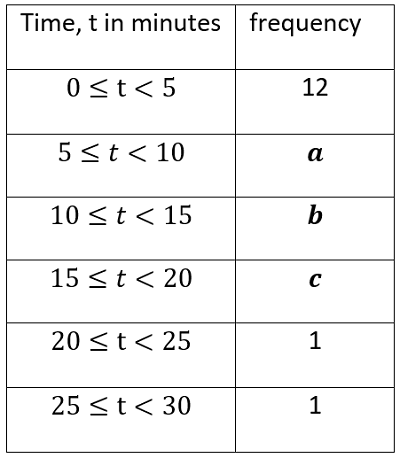




 a) Complete the probability tree for Katniss’s three attempts.
a) Complete the probability tree for Katniss’s three attempts.


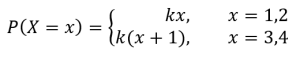

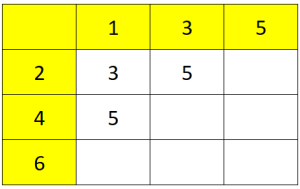


 A glass contains 5 green sweets and m sweets of other colours. A sweet is taken at random.
A glass contains 5 green sweets and m sweets of other colours. A sweet is taken at random.


 Twitter
Twitter  Facebook
Facebook  LinkedIn
LinkedIn