1.2.7 Standard Solutions

Standard solutions

• Chemists routinely prepare solutions needed for analysis, whose concentrations are known precisely
• These solutions are termed standard solutions
• They are made as accurately and precisely as possible using three decimal place balances and volumetric flasks to reduce the impact of measurement uncertainties
• The steps are:

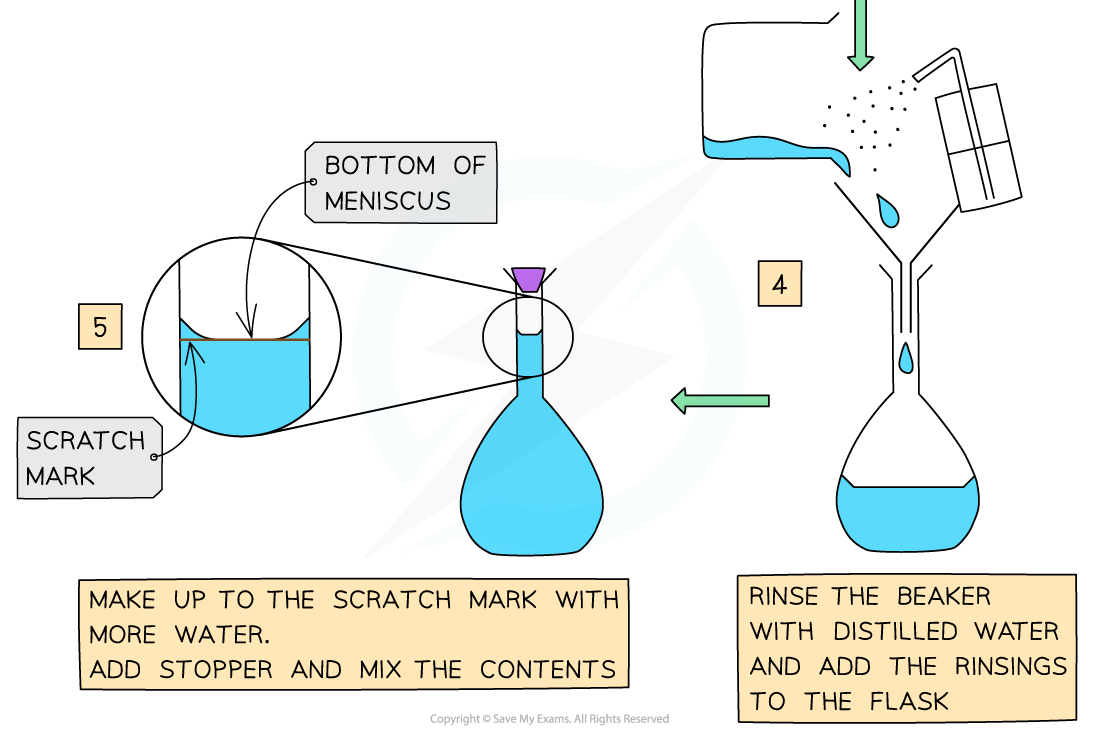
Volumes & concentrations of solutions

• The concentration of a solution is the amount of solute dissolved in a solvent to make 1 dm³ of  solution
  • The solute is the substance that dissolves in a solvent to form a solution
  • The solvent is often water

• A concentrated solution is a solution that has a high concentration of solute
• A dilute solution is a solution with a low concentration of solute
• Concentration is usually expressed in one of three ways:
  • moles per unit volume
  • mass per unit volume
  • parts per million

Moles per unit volume

• The formula for expressing concentration using moles is:

• You must make sure you change cm³ to dm³  (by dividing by 1000)
• The relationships can be expressed using this formula triangle:

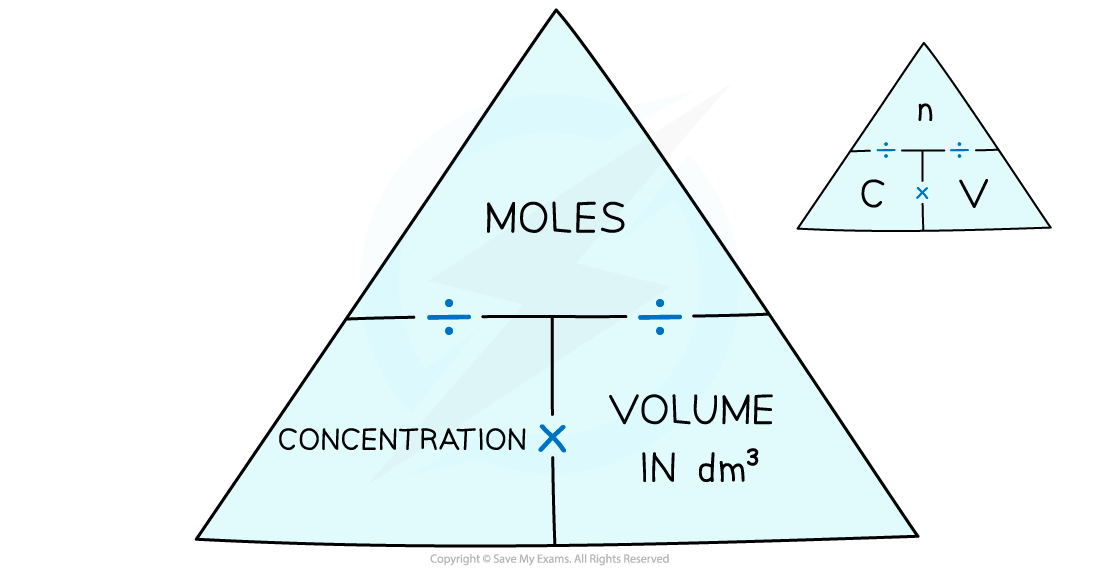
To use the concentration formula triangle cover the one you want to find out about with your finger and follow the instructions

Answer:

Step 1: Use the formula triangle to find the number of moles of NaOH needed

number of moles  = concentration (mol dm^-3) x volume (dm³)  

n = 0.200 mol dm^-3 x 0.250 dm³

n = 0.0500 mol

Step 2: Find the molar mass of NaOH

M = 22.99 + 16.00 + 1.01 = 40.00 g mol^-1

Step 3: Calculate the mass required

mass = moles x molar mass

mass =  0.0500 mol x 40.00 g mol^-1   = 2.00 g

Mass per unit volume

• Sometimes it is more convenient to express concentration in terms of mass per unit volume
• The formula is:

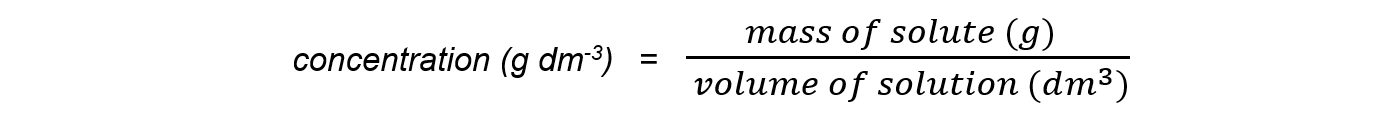
• To change a concentration from mol dm^-3 to g dm^-3  
  • Multiply the moles of solute by its molar mass

mass of solute (g) = number of moles (mol) x molar mass (g mol^-1)

Parts per million

• When expressing extremely low concentrations a unit that can be used is parts per million or ppm
• This is useful when giving the concentration of a pollutant in water or the air when the absolute amount is tiny compared the the volume of water or air
• 1 ppm is defined as
  • A mass of 1 mg dissolved in 1 dm³ of water
• Since 1 dm³ weighs 1 kg we can also say it is
  • A mass of 1 mg dissolved in 1 kg of water, or 10^-3 g in 10³ g which is the same as saying the concentration is 1 in 10⁶ or 1 in a million

Answer:

Step 1: calculate the total mass in mg assuming 3ppm(1 litre is the same as 1 dm³)

3 x 2.5 x 10⁶ = 7.5 x 10⁶ mg

Step 2: convert the mass into kilograms (1 mg = 10^-6 kg)

7.5 x 10⁶  x 10^-6  kg = 7.5 kg