IB Questionbank

Updates to Questionbank

User interface language: English | Español

Date	May 2022	Marks available	4	Reference code	22M.2.AHL.TZ1.6
Level	Additional Higher Level	Paper	Paper 2	Time zone	Time zone 1
Command term	Solve	Question number	6	Adapted from	N/A

Question

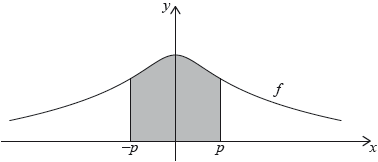
Consider the function $f (x) = 2^{x} - \frac{1}{2^{x}}, x \in ℝ$ .

The function $g$ is given by $g (x) = \frac{x - 1}{x^{2} - 2 x - 3}$ , where $x \in ℝ, x \neq - 1, x \neq 3$ .

Show that $f$ is an odd function.

[2]

a.

Solve the inequality $f (x) \geq g (x)$ .

[4]

b.

Markscheme

attempt to replace $x$ with $- x$ M1

$f (- x) = 2^{- x} - \frac{1}{2^{- x}}$

EITHER

$= \frac{1}{2^{x}} - 2^{x} = - f (x)$ A1

OR

$= - (2^{x} - \frac{1}{2^{x}}) (= - f (x))$ A1

Note: Award M1A0 for a graphical approach including evidence that either the graph is invariant after rotation by $180 °$ about the origin or the graph is invariant after a reflection in the $y$ -axis and then in the $x$ -axis (or vice versa).

so $f$ is an odd function AG

[2 marks]

a.

attempt to find at least one intersection point (M1)

$x = - 1.26686 \dots, x = 0.177935 \dots, x = 3.06167 \dots$

$x = - 1.27, x = 0.178, x = 3.06$

$- 1.27 \leq x \leq - 1,$ A1

$0.178 \leq x < 3,$ A1

$x \geq 3.06$ A1

[4 marks]

b.

Examiners report

[N/A]

a.

[N/A]

b.

Syllabus sections

Topic 2—Functions » SL 2.10—Solving equations graphically and analytically

Show 56 related questions

SPM.2.SL.TZ0.9a:
Find the period of $f$ .
22M.2.SL.TZ2.8b:
Find the values of $t$ when $h_{A} (t) = h_{B} (t)$ .
22M.2.AHL.TZ2.10d:
For $0 \leq t \leq 9$ , find the total amount of time when the rate of growth of Plant $B$ was greater than the rate of growth of Plant $A$ .
22M.2.AHL.TZ2.11d.ii:
Determine the length of time between the first airplane arriving at $P$ and the second airplane arriving at $P$ .
17M.2.SL.TZ2.S_10b.i:
Write down the probability of drawing three blue marbles.
18M.2.SL.TZ1.S_1c:
Solve f '(x) = f "(x).
17M.2.SL.TZ2.S_10b.iii:
The bag contains a total of ten marbles of which $w$ are white. Find $w$ .
17M.2.SL.TZ2.S_10d:
Grant plays the game until he wins two prizes. Find the probability that he wins his second prize on his eighth attempt.
19N.1.SL.TZ0.S_9a.i:
$\overrightarrow {{\text{OA}}} \bullet \overrightarrow {{\text{OC}}}$ .
19N.2.SL.TZ0.S_9a:
Calculate the probability a flight is not late.
19N.2.SL.TZ0.S_10c:
During the second stage, the rocket accelerates at a constant rate. The distance which the rocket travels during the second stage is the same as the distance it travels during the first stage.

Find the total time taken for the two stages.
19N.2.SL.TZ0.S_2b:
Write down a direction vector for ${L_3}$ .
19N.1.SL.TZ0.S_10c:
The line ${L_2}$ is tangent to the graph of $g$ at ${\text{A}}$ and has equation $y = \left( {{\text{ln}}\,p} \right)x + q + 1$ .

The line ${L_2}$ passes through the point $\left( { - 2{\text{, }} - 2} \right)$ .

The gradient of the normal to $g$ at ${\text{A}}$ is $\frac{1}{{{\text{ln}}\left( {\frac{1}{3}} \right)}}$ .

Find the equation of ${L_1}$ in terms of $x$ .
17M.1.SL.TZ1.S_10b:
Given that $\tan \theta > 0$ , find $\tan \theta$ .
19N.1.SL.TZ0.S_10a:
Write down the coordinates of ${\text{B}}$ .
18N.1.SL.TZ0.S_5:
Consider the vectors a = $\left( {\begin{array}{*{20}{c}} 3 \\ {2p} \end{array}} \right)$ and b = $\left( {\begin{array}{*{20}{c}} {p + 1} \\ 8 \end{array}} \right)$ .

Find the possible values of p for which a and b are parallel.
19M.2.SL.TZ2.S_4c:
Given that the area of triangle OBC is $\frac{3}{5}$ of the area of sector OAB, find θ.
17M.2.SL.TZ2.S_10a.i:
Find $q$ .
18M.2.SL.TZ1.S_7b:
Hence find the value of n such that $\sum\limits_{k = 1}^n {{x_k} = 861}$ .
18M.2.SL.TZ1.S_7a:
Given that x_k_{+ 1} = x_k + a, find a.
17N.2.SL.TZ0.S_5b:
The following diagram shows part of the graph of $f$ .

The region enclosed by the graph of $f$ , the $x$ -axis and the lines $x = - p$ and $x = p$ is rotated 360° about the $x$ -axis. Find the volume of the solid formed.
17M.1.SL.TZ1.S_10c:
Let $y = \frac{1}{{\cos x}}$ , for $0 < x < \frac{\pi }{2}$ . The graph of $y$ between $x = \theta$ and $x = \frac{\pi }{4}$ is rotated 360° about the $x$ -axis. Find the volume of the solid formed.
19N.2.SL.TZ0.S_9c.ii:
Given that at least $7$ of these flights are on time, find the probability that exactly $10$ flights are on time.
19N.2.SL.TZ0.S_9b:
Find the value of $m$ .
17N.2.SL.TZ0.S_5a:
Find the value of $p$ .
19N.1.SL.TZ0.S_9a.ii:
$\overrightarrow {{\text{OB}}} \bullet \overrightarrow {{\text{OC}}}$ .
22M.1.AHL.TZ2.3c:
Hence, solve the inequality $0 < \frac{2 x - 1}{x + 1} < 2$ .
22M.2.SL.TZ2.6b:
Find the times when the particle’s acceleration is $- 1.9 {m s}^{- 2}$ .
22M.2.SL.TZ2.6c:
Find the particle’s acceleration when its speed is at its greatest.
22M.2.SL.TZ2.8c:
For $0 \leq t \leq 9$ , find the total amount of time when the rate of growth of Plant $B$ was greater than the rate of growth of Plant $A$ .
22M.2.AHL.TZ2.11d.i:
Find the coordinates of $P$ .
22M.2.AHL.TZ2.12f:
After $10$ years, the population of marsupials is $3 P_{0}$ . It is known that $N = 4 P_{0}$ .

Find the value of $k$ for this population model.
19N.2.SL.TZ0.S_9d:
SpeedWay increases the number of flights from city ${\text{A}}$ to city ${\text{B}}$ to $20$ flights each week, and improves their efficiency so that more flights are on time. The probability that at least $19$ flights are on time is $0.788$ .

A flight is chosen at random. Calculate the probability that it is on time.
17M.2.SL.TZ2.S_10c:
Jill plays the game nine times. Find the probability that she wins exactly two prizes.
16N.2.SL.TZ0.S_4b:
Hence, find the area of the region enclosed by the graphs of $f$ and $g$ .
17N.1.SL.TZ0.S_8d:
Find the area of the region enclosed by the graph of $f$ and the line $L$ .
19N.2.SL.TZ0.S_2c:
${L_3}$ passes through the intersection of ${L_1}$ and ${L_2}$ .

Write down a vector equation for ${L_3}$ .
SPM.2.SL.TZ0.9b.ii:
Hence, find the value of $f$ (6).
19N.1.SL.TZ0.S_9b:
Given that ${\text{A}}\widehat {\text{O}}{\text{C}} = {\text{B}}\widehat {\text{O}}{\text{C}}$ , show that $k = 7$ .
SPM.2.SL.TZ0.9b.i:
Find the value of $b$ .
19M.2.SL.TZ2.S_4a:
Show that ${\text{OC}} = r\,{\text{cos}}\,\theta$ .
19N.2.SL.TZ0.S_9c.i:
Calculate the probability that at least $7$ of these flights are on time.
19N.1.SL.TZ0.S_10b:
Given that $f'\left( a \right) = \frac{1}{{{\text{ln}}\,p}}$ , find the equation of ${L_1}$ in terms of $x$ , $p$ and $q$ .
17M.2.SL.TZ2.S_10b.ii:
Explain why the probability of drawing three white marbles is $\frac{1}{6}$ .
19N.2.SL.TZ0.S_10b:
Find the distance that the rocket travels during the first stage.
19N.2.SL.TZ0.S_2a:
Find the point of intersection of ${L_1}$ and ${L_2}$ .
22M.1.SL.TZ2.8a:
Find the coordinates of $B$ .
17M.2.SL.TZ2.S_10a.ii:
Find $p$ .
19M.2.SL.TZ2.S_4b:
Find the area of triangle OBC in terms of $r$ and θ.
19N.2.SL.TZ0.S_10a:
Find an expression for the velocity, $v$ m s⁻¹, of the rocket during the first stage.
17M.1.SL.TZ1.S_10a:
Show that $\cos \theta = \frac{3}{4}$ .
16N.1.AHL.TZ0.H_5:
The quadratic equation ${x^2} - 2kx + (k - 1) = 0$ has roots $\alpha$ and $\beta$ such that ${\alpha ^2} + {\beta ^2} = 4$ . Without solving the equation, find the possible values of the real number $k$ .
16N.2.SL.TZ0.S_4a:
Find the value of $p$ and of $q$ .
19N.1.SL.TZ0.S_9c:
Calculate the area of triangle ${\text{AOC}}$ .
SPM.2.SL.TZ0.9d:
Find the value of $x$ for which the functions have the greatest difference.
SPM.2.SL.TZ0.9c:
Find the value of $p$ and the value of $q$ .

Hide related questions

Topic 2—Functions » AHL 2.13—Rational functions

Topic 2—Functions » AHL 2.15—Solutions of inequalities

Topic 2—Functions