| Date | November 2013 | Marks available | 3 | Reference code | 13N.1.hl.TZ0.10 |
| Level | HL only | Paper | 1 | Time zone | TZ0 |
| Command term | Find and Hence | Question number | 10 | Adapted from | N/A |
Question
The function \(f\) is given by \(f(x) = x{{\text{e}}^{ - x}}{\text{ }}(x \geqslant 0)\).
(i) Find an expression for \(f'(x)\).
(ii) Hence determine the coordinates of the point A, where \(f'(x) = 0\).
Find an expression for \(f''(x)\) and hence show the point A is a maximum.
Find the coordinates of B, the point of inflexion.
The graph of the function \(g\) is obtained from the graph of \(f\) by stretching it in the x-direction by a scale factor 2.
(i) Write down an expression for \(g(x)\).
(ii) State the coordinates of the maximum C of \(g\).
(iii) Determine the x-coordinates of D and E, the two points where \(f(x) = g(x)\).
Sketch the graphs of \(y = f(x)\) and \(y = g(x)\) on the same axes, showing clearly the points A, B, C, D and E.
Find an exact value for the area of the region bounded by the curve \(y = g(x)\), the x-axis and the line \(x = 1\).
Markscheme
(i) \(f'(x) = {{\text{e}}^{ - x}} - x{{\text{e}}^{ - x}}\) M1A1
(ii) \(f'(x) = 0 \Rightarrow x = 1\)
coordinates \(\left( {1,{\text{ }}{{\text{e}}^{ - 1}}} \right)\) A1
[3 marks]
\(f''(x) = - {{\text{e}}^{ - x}} - {{\text{e}}^{ - x}} + x{{\text{e}}^{ - x}}{\text{ }}\left( { = - {{\text{e}}^{ - x}}(2 - x)} \right)\) A1
substituting \(x = 1\) into \(f''(x)\) M1
\(f''(1){\text{ }}\left( { = - {{\text{e}}^{ - 1}}} \right) < 0\) hence maximum R1AG
[3 marks]
\(f''(x) = 0{\text{ (}} \Rightarrow x = 2)\) M1
coordinates \(\left( {2,{\text{ 2}}{{\text{e}}^{ - 2}}} \right)\) A1
[2 marks]
(i) \(g(x) = \frac{x}{2}{{\text{e}}^{ - \frac{x}{2}}}\) A1
(ii) coordinates of maximum \(\left( {2,{\text{ }}{{\text{e}}^{ - 1}}} \right)\) A1
(iii) equating \(f(x) = g(x)\) and attempting to solve \(x{{\text{e}}^{ - x}} = \frac{x}{2}{{\text{e}}^{ - \frac{x}{2}}}\)
\( \Rightarrow x\left( {2{{\text{e}}^{\frac{x}{2}}} - {{\text{e}}^x}} \right) = 0\) (A1)
\( \Rightarrow x = 0\) A1
or \(2{{\text{e}}^{\frac{x}{2}}} = {{\text{e}}^x}\)
\( \Rightarrow {{\text{e}}^{\frac{x}{2}}} = 2\)
\( \Rightarrow x = 2\ln 2\) \((\ln 4)\) A1
Note: Award first (A1) only if factorisation seen or if two correct
solutions are seen.
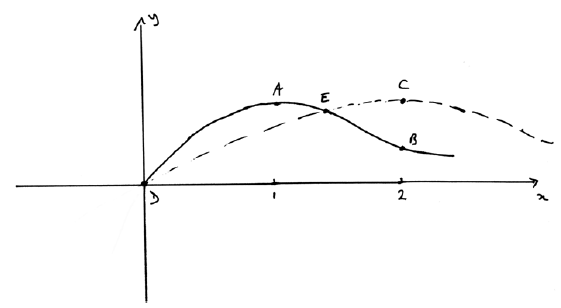 A4
A4
Note: Award A1 for shape of \(f\), including domain extending beyond \(x = 2\).
Ignore any graph shown for \(x < 0\).
Award A1 for A and B correctly identified.
Award A1 for shape of \(g\), including domain extending beyond \(x = 2\).
Ignore any graph shown for \(x < 0\). Allow follow through from \(f\).
Award A1 for C, D and E correctly identified (D and E are interchangeable).
[4 marks]
\(A = \int_0^1 {\frac{x}{2}{{\text{e}}^{ - \frac{x}{2}}}{\text{d}}x} \) M1
\( = \left[ { - x{{\text{e}}^{ - \frac{x}{2}}}} \right]_0^1 - \int_0^1 { - {{\text{e}}^{ - \frac{x}{2}}}{\text{d}}x} \) A1
Note: Condone absence of limits or incorrect limits.
\( = - {{\text{e}}^{ - \frac{1}{2}}} - \left[ {2{{\text{e}}^{ - \frac{x}{2}}}} \right]_0^1\)
\( = - {{\text{e}}^{ - \frac{1}{2}}} - \left( {2{{\text{e}}^{ - \frac{1}{2}}} - 2} \right) = 2 - 3{{\text{e}}^{ - \frac{1}{2}}}\) A1
[3 marks]
Examiners report
Part a) proved to be an easy start for the vast majority of candidates.
Full marks for part b) were again likewise seen, though a small number shied away from considering the sign of their second derivative, despite the question asking them to do so.
Part c) again proved to be an easily earned 2 marks.
Full marks for part b) were again likewise seen, though a small number shied away from considering the sign of their second derivative, despite the question asking them to do so.
Part c) again proved to be an easily earned 2 marks.
Many candidates lost their way in part d). A variety of possibilities for \(g(x)\) were suggested, commonly \(2x{{\text{e}}^{ - 2x}}\), \(\frac{{x{{\text{e}}^{ - 1}}}}{2}\) or similar variations. Despite section ii) being worth only one mark, (and ‘state’ being present in the question), many laborious attempts at further differentiation were seen. Part diii was usually answered well by those who gave the correct function for \(g(x)\).
Part e) was also answered well by those who had earned full marks up to that point.
While the integration by parts technique was clearly understood, it was somewhat surprising how many careless slips were seen in this part of the question. Only a minority gained full marks for part f).

