| Date | May 2018 | Marks available | 4 | Reference code | 18M.3.SL.TZ2.1 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | Calculate | Question number | 1 | Adapted from | N/A |
Question
To determine the acceleration due to gravity, a small metal sphere is dropped from rest and the time it takes to fall through a known distance and open a trapdoor is measured.
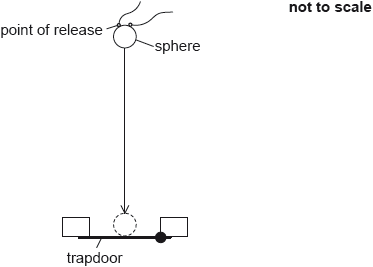
The following data are available.
\[\begin{array}{*{20}{l}} {{\text{Diameter of metal sphere}}}&{ = 12.0 \pm 0.1{\text{ mm}}} \\ {{\text{Distance between the point of release and the trapdoor}}}&{ = 654 \pm 2{\text{ mm}}} \\ {{\text{Measured time for fall}}}&{ = 0.363 \pm 0.002{\text{ s}}} \end{array}\]
Determine the distance fallen, in m, by the centre of mass of the sphere including an estimate of the absolute uncertainty in your answer.
Using the following equation
\[{\text{acceleration due to gravity}} = \frac{{2 \times {\text{distance fallen by centre of mass of sphere}}}}{{{{{\text{(measured time to fall)}}}^{\text{2}}}}}\]
calculate, for these data, the acceleration due to gravity including an estimate of the absolute uncertainty in your answer.
Markscheme
distance fallen = 654 – 12 = 642 «mm»
absolute uncertainty = 2 + 0.1 «mm» ≈ 2 × 10–3 «m» or = 2.1 × 10–3 «m» or 2.0 × 10–3 «m»
Accept answers in mm or m
[2 marks]
«a = \(\frac{{2s}}{{{t^2}}} = \frac{{2 \times 0.642}}{{{{0.363}^2}}}\)» = 9.744 «ms–2»
fractional uncertainty in distance = \(\frac{2}{{642}}\) AND fractional uncertainty in time = \(\frac{{0.002}}{{0.363}}\)
total fractional uncertainty = \(\frac{{\Delta s}}{s} + 2\frac{{\Delta t}}{t}\) «= 0.00311 + 2 × 0.00551»
total absolute uncertainty = 0.1 or 0.14 AND same number of decimal places in value and uncertainty, ie: 9.7 ± 0.1 or 9.74 ± 0.14
Accept working in % for MP2 and MP3
Final uncertainty must be the absolute uncertainty
[4 marks]

