| Date | November 2010 | Marks available | 3 | Reference code | 10N.2.SL.TZ0.A1 |
| Level | Standard level | Paper | Paper 2 | Time zone | Time zone 0 |
| Command term | Calculate | Question number | A1 | Adapted from | N/A |
Question
A student performs an experiment with a paper toy that rotates as it falls slowly through the air. After release, the paper toy quickly attains a constant vertical speed as measured over a fixed vertical distance.
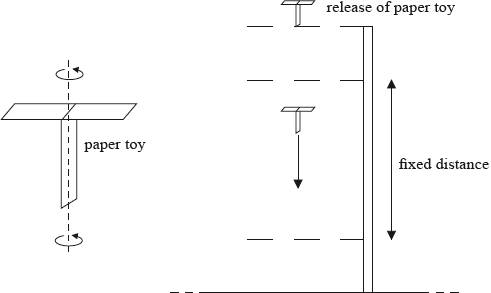
The aim of the experiment was to find how the terminal speed of the paper toy varies with its weight. The weight of the paper toy was changed by using different numbers of paper sheets in its construction.
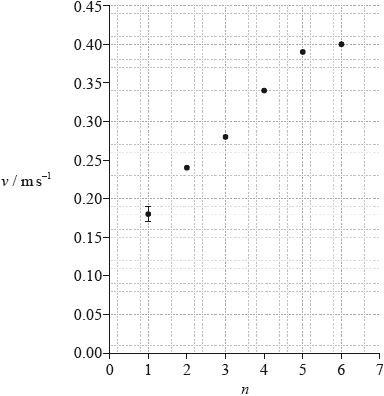
The graph shows a plot of the terminal speed \(v\) of the paper toy (calculated from the raw data) and the number of paper sheets \(n\) used to construct the toy. The uncertainty in \(v\) for \(n = 1\) is shown by the error bar.
The fixed distance is 0.75 m and has an absolute uncertainty of 0.01 m. The percentage uncertainty in the time taken to fall through the fixed distance is 5%.
Calculate the absolute uncertainty in the terminal speed of the paper toy for \(n = 6\).
On the graph, draw an error bar on the point corresponding to \(n = 6\).
On the graph, draw a line of best-fit for the data points.
The student hypothesizes that v is proportional to n. Use the data points for \(n = 2\) and \(n = 4\) from the graph opposite to show that this hypothesis is incorrect.
Another student hypothesized that \(v\) might be proportional to \(n\). To verify this hypothesis he plotted a graph of \({v^2}\) against \(\sqrt n \) as shown below.
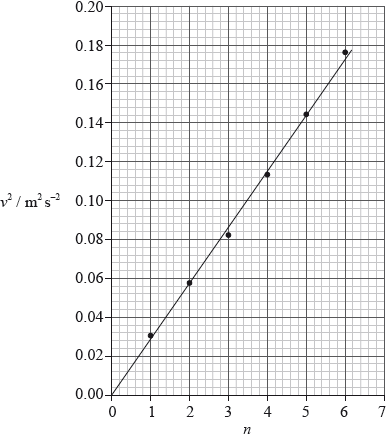
Explain how the graph verifies the hypothesis that \(v\) is proportional to \(\sqrt n \).
Markscheme
percentage uncertainty in distance \(\left( {\frac{{0.01}}{{0.75}} = } \right){\text{ }}1.3\% \);
percentage uncertainty in \(v = (5 + 1.3 = ){\text{ }}6.3\% \);
absolute uncertainty in \(n = 6\) point is \((0.40 \times 0.063{\text{ = }}){\text{ }}0.025{\text{ m}}\,{{\text{s}}^{ - 1}}\);
overall length of error bar drawn correct to within half a small square;
Consistent with (a)(i).
any reasonable smooth curve/straight-line passing through error bars
Do not award where abrupt change of gradient occurs at n = 5.
tests for \(\frac{v}{n}\) or \(\frac{n}{v}\);
\(\frac{v}{n} = 0.12\) for \(n = 2\) and \(\frac{v}{n} = 0.085\) for \(n = 4\); (both needed)
hypothesis incorrect because two values should be equal;
Accept for [3] read-off of both 0.24 and 0.34 together with the comment that 0.34 is not double 0.24.
Award [2 max] if no use of data but candidate has drawn curve with no straight portion and comments that line is not straight and does not go through origin.
Award [1 max] if no use of data but candidate has drawn a straight line and comments that line is straight but not through origin.
\(\left( {{\text{if }}v \propto \sqrt n } \right){v^2} \propto n\);
graph of \({v^2}\) against \(n\) is a straight-line;
that goes through the origin;
Examiners report
This was well done with almost all candidates understanding the combination of errors.
Only the weakest candidates could not take the uncertainty value calculated in (a)(i) and transfer this correctly to the graph.
This was not well done. Too many candidates forced their lines through the printed origin, drew lines that lay outside the two error bars at each end of the range, or gave unrealistic abrupt changes of gradient.
Many understood the need to compare ratios in some way and identify that the ratios were not the same for \(n = 2\) or 4. However, some candidates appeared unable to make any attempt at this question.
This is an example of a case where a clear and logical presentation is required so that examiners can understand what is in the candidate‟s mind.

