| Date | May 2018 | Marks available | 4 | Reference code | 18M.3.SL.TZ2.2 |
| Level | Standard level | Paper | Paper 3 | Time zone | Time zone 2 |
| Command term | Determine | Question number | 2 | Adapted from | N/A |
Question
A student carries out an experiment to determine the variation of intensity of the light with distance from a point light source. The light source is at the centre of a transparent spherical cover of radius C. The student measures the distance x from the surface of the cover to a sensor that measures the intensity I of the light.
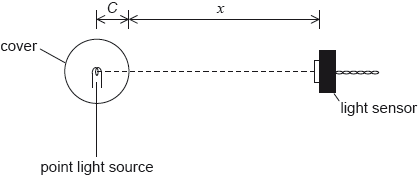
The light source emits radiation with a constant power P and all of this radiation is transmitted through the cover. The relationship between I and x is given by
\[I = \frac{P}{{4\pi {{(C + x)}^2}}}\]
The student obtains a set of data and uses this to plot a graph of the variation of \(\frac{1}{{\sqrt I }}\) with x.
This relationship can also be written as follows.
\[\frac{1}{{\sqrt I }} = Kx + KC\]
Show that \(K = 2\sqrt {\frac{\pi }{P}} \).
Estimate C.
Determine P, to the correct number of significant figures including its unit.
Explain the disadvantage that a graph of I versus \(\frac{1}{{{x^2}}}\) has for the analysis in (b)(i) and (b)(ii).
Markscheme
combines the two equations to obtain result
«for example \(\frac{1}{I}\) = K2(C + x)2 = \(\frac{{4\pi }}{P}\)(C + x)2»
OR
reverse engineered solution – substitute K = \(2\sqrt {\frac{\pi }{P}} \) into \(\frac{1}{I}\) = K2(C + x)2 to get I = \(\frac{P}{{4\pi {{(C + x)}^2}}}\)
There are many ways to answer the question, look for a combination of two equations to obtain the third one
[1 mark]
extrapolating line to cross x-axis / use of x-intercept
OR
Use C = \(\frac{{y{\text{ - intercept}}}}{{{\text{gradient}}}}\)
OR
use of gradient and one point, correctly substituted in one of the formulae
accept answers between 3.0 and 4.5 «cm»
Award [1 max] for negative answers
[2 marks]
ALTERNATIVE 1
Evidence of finding gradient using two points on the line at least 10 cm apart
Gradient found in range: 115–135 or 1.15–1.35
Using P = \(\frac{{4\pi }}{{{K^2}}}\) to get value between 6.9 × 10–4 and 9.5 × 10–4 «W» and POT correct
Correct unit, W and answer to 1, 2 or 3 significant figures
ALTERNATIVE 2
Finds \(I\left( {\frac{1}{{{y^2}}}} \right)\) from use of one point (x and y) on the line with x > 6 cm and C from(b)(i)to use in I = \(\frac{P}{{4\pi {{(C + x)}^2}}}\) or \(\frac{1}{{\sqrt I }}\) = Kx + KC
Correct re-arrangementto get P between 6.9 × 10–4 and 9.5 × 10–4 «W» and POT correct
Correct unit, W and answer to 1, 2 or 3 significant figures
Award [3 max] for an answer between 6.9 W and 9.5 W (POT penalized in 3rd marking point)
Alternative 2 is worth [3 max]
[4 marks]
this graph will be a curve / not be a straight line
more difficult to determine value of K
OR
more difficult to determine value of C
OR
suitable mathematical argument
OWTTE
[2 marks]

