| Date | May 2013 | Marks available | 1 | Reference code | 13M.2.sl.TZ2.1 |
| Level | SL | Paper | 2 | Time zone | TZ2 |
| Command term | Deduce | Question number | 1 | Adapted from | N/A |
Question
Iron tablets are often prescribed to patients. The iron in the tablets is commonly present as iron(II) sulfate, \({\text{FeS}}{{\text{O}}_{\text{4}}}\).
Two students carried out an experiment to determine the percentage by mass of iron in a brand of tablets marketed in Cyprus.
Experimental Procedure:
• The students took five iron tablets and found that the total mass was 1.65 g.
• The five tablets were ground and dissolved in \({\text{100 c}}{{\text{m}}^{\text{3}}}\) dilute sulfuric acid, \({{\text{H}}_{\text{2}}}{\text{S}}{{\text{O}}_{\text{4}}}{\text{(aq)}}\). The solution and washings were transferred to a \({\text{250 c}}{{\text{m}}^{\text{3}}}\) volumetric flask and made up to the mark with deionized (distilled) water.
• \({\text{25.0 c}}{{\text{m}}^{\text{3}}}\) of this \({\text{F}}{{\text{e}}^{2 + }}{\text{(aq)}}\) solution was transferred using a pipette into a conical flask. Some dilute sulfuric acid was added.
• A titration was then carried out using a \(5.00 \times {10^{ - 3}}{\text{ mol}}\,{\text{d}}{{\text{m}}^{ - 3}}\) standard solution of potassium permanganate, \({\text{KMn}}{{\text{O}}_{\text{4}}}{\text{(aq)}}\). The end-point of the titration was indicated by a slight pink colour.
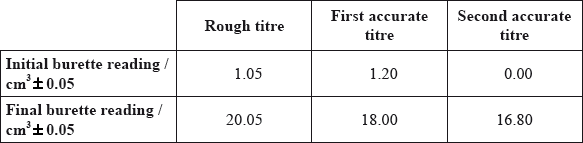
The following results were recorded.
This experiment involves the following redox reaction.
\[{\text{5F}}{{\text{e}}^{2 + }}{\text{(aq)}} + {\text{MnO}}_4^ - {\text{(aq)}} + {\text{8}}{{\text{H}}^ + }{\text{(aq)}} \to {\text{5F}}{{\text{e}}^{3 + }}{\text{(aq)}} + {\text{M}}{{\text{n}}^{2 + }}{\text{(aq)}} + {\text{4}}{{\text{H}}_2}{\text{O(l)}}\]
When the \({\text{F}}{{\text{e}}^{2 + }}{\text{(aq)}}\) solution was made up in the \({\text{250 c}}{{\text{m}}^{\text{3}}}\) volumetric flask, deionized (distilled) water was added until the bottom of its meniscus corresponded to the graduation mark on the flask. It was noticed that one of the two students measured the volume of the solution from the top of the meniscus instead of from the bottom. State the name of this type of error.
State what is meant by the term precision.
When the students recorded the burette readings, following the titration with KMnO4 (aq),the top of the meniscus was used and not the bottom. Suggest why the students read the top of the meniscus and not the bottom.
Define the term reduction in terms of electrons.
Deduce the oxidation number of manganese in the \({\text{MnO}}_{\text{4}}^ - {\text{(aq)}}\) ion.
Determine the amount, in mol, of \({\text{MnO}}_{\text{4}}^ - {\text{(aq)}}\), used in each accurate titre.
Calculate the amount, in mol, of \({\text{F}}{{\text{e}}^{2 + }}{\text{(aq)}}\) ions in \({\text{250 c}}{{\text{m}}^{\text{3}}}\) of the solution.
Determine the total mass of iron, in g, in the \({\text{250 c}}{{\text{m}}^{\text{3}}}\) solution.
Determine the percentage by mass of iron in the tablets.
One titration was abandoned because a brown precipitate, manganese(IV) oxide, formed. State the chemical formula of this compound.
Markscheme
systematic (error);
Do not accept parallax.
closeness of agreement of a set of measurements to each other / OWTTE;
Allow reproducibility/consistency of measurement / measurements with small random errors/total amount of random errors/standard deviation / a more precise value contains more significant figures / OWTTE.
potassium permanganate has a very dark/deep (purple) colour so cannot read bottom of meniscus / OWTTE;
gain (of electrons);
VII / +7;
Do not accept 7 or 7+.
volume \( = 16.80{\text{ }}({\text{c}}{{\text{m}}^3})/18.00 - 1.20{\text{ }}({\text{c}}{{\text{m}}^3})\);
amount \(\left( { = \frac{{16.80 \times 5.00 \times {{10}^{ - 3}}}}{{1000}}} \right) = 8.40 \times {10^{ - 5}}{\text{ (mol)}}\);
Award [2] for correct final answer.
\((8.40 \times {10^{ - 5}} \times 5 \times 10) = 4.20 \times {10^{ - 3}}{\text{ (mol per 250 c}}{{\text{m}}^{\text{3}}}{\text{)}}\);
\((55.85 \times 4.20 \times {10^{ - 3}}) = 0.235{\text{ (g)}}\);
Do not penalize if 56 g mol–1 is used for atomic mass of iron.
\(\left( {\frac{{{\text{0.235}} \times {\text{100}}}}{{{\text{1.65}}}} = } \right){\text{ 14.2% }}\);
No ECF if answer >100 %.
MnO2;
Examiners report
Question 1 presented difficulties to many candidates. It is felt that the extended nature of the response distracted candidates from rather straight-forward quantitative chemistry calculations. Part (a) required candidates to determine whether an error was systematic or random and part (b) asked for the meaning of precision. Both of these questions are relevant to Topic 11.
Question 1 presented difficulties to many candidates. It is felt that the extended nature of the response distracted candidates from rather straight-forward quantitative chemistry calculations. Part (a) required candidates to determine whether an error was systematic or random and part (b) asked for the meaning of precision. Both of these questions are relevant to Topic 11.
Very few candidates related reading the top of the meniscus in the burette in part (c) to the colour of the KMnO4 solution. While it is acknowledged that few candidates would have performed this experiment themselves, it is reasonable that candidates should know the colour of KMnO4.
Part d) (i) was answered very well with nearly all candidates correctly defining reduction.
In d) (ii) many candidates correctly deduced the oxidation number of Mn in MnO4. Several lost marks, however, for not using acceptable notation. 7 by itself is not correct.
Part (e) involved the calculations. Candidates were guided through the process of calculating number of moles from concentration and volume, finding mole ratios, and determining mass from moles and molar mass. Better candidates performed these calculations well. Weaker candidates often scored follow-through marks when working was shown.
Part (e) involved the calculations. Candidates were guided through the process of calculating number of moles from concentration and volume, finding mole ratios, and determining mass from moles and molar mass. Better candidates performed these calculations well. Weaker candidates often scored follow-through marks when working was shown.
Part (e) involved the calculations. Candidates were guided through the process of calculating number of moles from concentration and volume, finding mole ratios, and determining mass from moles and molar mass. Better candidates performed these calculations well. Weaker candidates often scored follow-through marks when working was shown.
Part (e) involved the calculations. Candidates were guided through the process of calculating number of moles from concentration and volume, finding mole ratios, and determining mass from moles and molar mass. Better candidates performed these calculations well. Weaker candidates often scored follow-through marks when working was shown.
In f) (i) a common error was to write Mn2O4 as the formula for manganese(IV) oxide. Also common was the use of the symbol Mg for manganese.

