| Date | May 2013 | Marks available | 3 | Reference code | 13M.2.hl.TZ2.2 |
| Level | HL | Paper | 2 | Time zone | TZ2 |
| Command term | Determine | Question number | 2 | Adapted from | N/A |
Question
Consider the following graph of \(\ln k\) against \(\frac{1}{T}\).
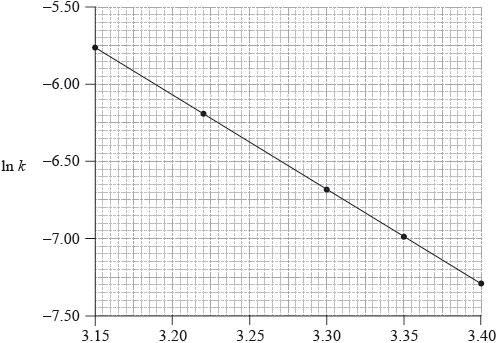
\[\frac{1}{T}/{10^{ - 3}}{\text{ }}{{\text{K}}^{ - 1}}\]
A catalyst provides an alternative pathway for a reaction, lowering the activation energy, \({E_{\text{a}}}\). Define the term activation energy, \({E_{\text{a}}}\).
State how the rate constant, k , varies with temperature, T.
Determine the activation energy, \({E_{\text{a}}}\), correct to three significant figures and state its units.
Markscheme
minimum energy needed (by reactants/colliding particles) to react/start/initiate a reaction / for a successful collision;
Allow energy difference between reactants and transition state.
k increases with T;
Do not accept k proportional to T or statement of Arrhenius equation from Data booklet.
slope/gradient/\(m = \frac{{ - {E_{\text{a}}}}}{R}/ - 6.20 \times {10^3}\);
Allow range of m from –5.96 \( \times \) 103 to –6.44 \( \times \) 103.
Award M1 for \(m = \frac{{ - {E_{\text{a}}}}}{R}\) even if gradient is out of range.
\({E_{\text{a}}} = (6.20 \times {10^3} \times 8.31) = 51.5{\text{ kJ}}\,{\text{mo}}{{\text{l}}^{ - 1}}/5.15 \times {10^4}{\text{ J}}\,{\text{mo}}{{\text{l}}^{ - 1}}\)
\({E_{\text{a}}}\) value correct;
units correct;
Award [3] for correct final answer.
Allow range of Ea from 49.5 to 53.5 kJ\(\,\)mol–1 / 4.95 \( \times \) 104 to 5.35 \( \times \) 104 J\(\,\)mol–1.
Answer must be given correct to three significant figures.
M3 can be scored independently.
Examiners report
In (a) the most common mistake was for students to omit minimum in the definition of activation energy. Many described the relation between temperature and rate constant as linear or ‘proportional’. Only a small number of students gained full marks for the determination of activation energy because many either calculated an incorrect gradient or used the wrong units.
In (a) the most common mistake was for students to omit minimum in the definition of activation energy. Many described the relation between temperature and rate constant as linear or ‘proportional’. Only a small number of students gained full marks for the determination of activation energy because many either calculated an incorrect gradient or used the wrong units.
In (a) the most common mistake was for students to omit minimum in the definition of activation energy. Many described the relation between temperature and rate constant as linear or ‘proportional’. Only a small number of students gained full marks for the determination of activation energy because many either calculated an incorrect gradient or used the wrong units.

