| Date | May 2014 | Marks available | 1 | Reference code | 14M.2.hl.TZ1.2 |
| Level | HL | Paper | 2 | Time zone | TZ1 |
| Command term | State | Question number | 2 | Adapted from | N/A |
Question
Sodium thiosulfate solution, \({\text{N}}{{\text{a}}_{\text{2}}}{{\text{S}}_{\text{2}}}{{\text{O}}_{\text{3}}}{\text{(aq)}}\), and hydrochloric acid, \({\text{HCl(aq)}}\), react to produce solid sulfur as in the equation below.
\[{{\text{S}}_2}{\text{O}}_3^{2 - }{\text{(aq)}} + {\text{2}}{{\text{H}}^ + }{\text{(aq)}} \to {\text{S(s)}} + {\text{S}}{{\text{O}}_2}{\text{(g)}} + {{\text{H}}_2}{\text{O(l)}}\]
The following results to determine the initial rate were obtained:
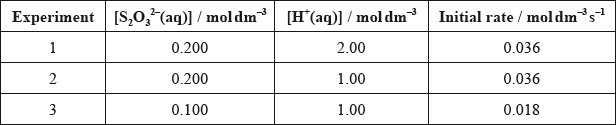
Deduce, with a reason, the order of reaction with respect to each reactant.
State the rate expression for this reaction.
Determine the value of the rate constant, \(k\), and state its units.
State an equation for a possible rate-determining step for the reaction.
Suggest how the activation energy, \({E_{\text{a}}}\), for this reaction may be determined.
Markscheme
experiments 1 and 2 (\({\text{[}}{{\text{S}}_2}{\text{O}}_3^{2 - }{\text{]}}\) remains constant) change in \({\text{[}}{{\text{H}}^ + }{\text{]}}\) does not affect the rate so zero order with respect to \({{\text{H}}^ + }{\text{(aq)}}\) / OWTTE;
experiment 1/2 and 3 (\({\text{[}}{{\text{H}}^ + }{\text{]}}\) has no effect) \({\text{[}}{{\text{S}}_2}{\text{O}}_3^{2 - }{\text{]}}\) is halved and rate is also halved so first order with respect to \({\text{[}}{{\text{S}}_2}{\text{O}}_3^{2 - }{\text{]}}\) / OWTTE;
Accept explanation given in mathematical terms.
Award [1 max] if both [S2O32–] is first order, and [H+] is zero order are stated without reason.
rate \( = k{\text{[}}{{\text{S}}_2}{\text{O}}_3^{2 - }{\text{]}}\);
0.18;
\({{\text{s}}^{ - 1}}\);
\({{\text{S}}_2}{\text{O}}_3^{2 - } \to {\text{S}} + {\text{SO}}_3^{2 - }\);
Accept any balanced equation that starts with only one S2O32–.
Equations must be balanced in terms of number of atoms and charge.
determine rate at a range of temperatures (while keeping concentrations constant);
calculate \(k\) for each temperature;
plot graph of \(\ln k\) against \({T^{ - {\text{1}}}}\);
gradient is \(\frac{{ - {E_{\text{a}}}}}{R}/\)OWTTE;
Examiners report
The interpretation of orders of rate from experimental data was well understood, and explained. Calculations of both the value and units of \({K_{\text{c}}}\) were also done well. Very few candidates produced an acceptable equation for the rate determining step, many did not realise the importance of balancing both the number of atoms and charge on both sides. The required careful explanation of how \({E_{\text{a}}}\) is determined from experimental data was lacking, too often a vague description of using gradient and \(R\) without context was considered sufficient by many candidates.
The interpretation of orders of rate from experimental data was well understood, and explained. Calculations of both the value and units of \({K_{\text{c}}}\) were also done well. Very few candidates produced an acceptable equation for the rate determining step, many did not realise the importance of balancing both the number of atoms and charge on both sides. The required careful explanation of how \({E_{\text{a}}}\) is determined from experimental data was lacking, too often a vague description of using gradient and \(R\) without context was considered sufficient by many candidates.
The interpretation of orders of rate from experimental data was well understood, and explained. Calculations of both the value and units of \({K_{\text{c}}}\) were also done well. Very few candidates produced an acceptable equation for the rate determining step, many did not realise the importance of balancing both the number of atoms and charge on both sides. The required careful explanation of how \({E_{\text{a}}}\) is determined from experimental data was lacking, too often a vague description of using gradient and \(R\) without context was considered sufficient by many candidates.
The interpretation of orders of rate from experimental data was well understood, and explained. Calculations of both the value and units of \({K_{\text{c}}}\) were also done well. Very few candidates produced an acceptable equation for the rate determining step, many did not realise the importance of balancing both the number of atoms and charge on both sides. The required careful explanation of how \({E_{\text{a}}}\) is determined from experimental data was lacking, too often a vague description of using gradient and \(R\) without context was considered sufficient by many candidates.
The interpretation of orders of rate from experimental data was well understood, and explained. Calculations of both the value and units of \({K_{\text{c}}}\) were also done well. Very few candidates produced an acceptable equation for the rate determining step, many did not realise the importance of balancing both the number of atoms and charge on both sides. The required careful explanation of how \({E_{\text{a}}}\) is determined from experimental data was lacking, too often a vague description of using gradient and \(R\) without context was considered sufficient by many candidates.

