| Date | May 2013 | Marks available | 2 | Reference code | 13M.1.sl.TZ2.10 |
| Level | SL only | Paper | 1 | Time zone | TZ2 |
| Command term | Explain why | Question number | 10 | Adapted from | N/A |
Question
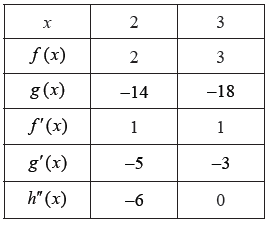
Consider the functions \(f(x)\) , \(g(x)\) and \(h(x)\) . The following table gives some values associated with these functions.
The following diagram shows parts of the graphs of \(h\) and \(h''\) .
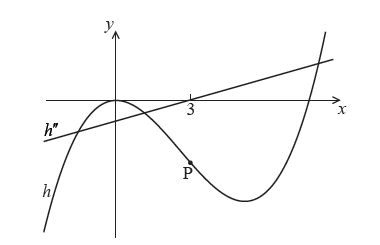
There is a point of inflexion on the graph of \(h\) at P, when \(x = 3\) .
Given that \(h(x) = f(x) \times g(x)\) ,
Write down the value of \(g(3)\) , of \(f'(3)\) , and of \(h''(2)\) .
Explain why P is a point of inflexion.
find the \(y\)-coordinate of P.
find the equation of the normal to the graph of \(h\) at P.
Markscheme
\(g(3) = - 18\) , \(f'(3) = 1\) , \(h''(2) = - 6\) A1A1A1 N3
[3 marks]
\(h''(3) = 0\) (A1)
valid reasoning R1
eg \({h''}\) changes sign at \(x = 3\) , change in concavity of \(h\) at \(x = 3\)
so P is a point of inflexion AG N0
[2 marks]
writing \(h(3)\) as a product of \(f(3)\) and \(g(3)\) A1
eg \(f(3) \times g(3)\) , \(3 \times ( - 18)\)
\(h(3) = - 54\) A1 N1
[2 marks]
recognizing need to find derivative of \(h\) (R1)
eg \({h'}\) , \(h'(3)\)
attempt to use the product rule (do not accept \(h' = f' \times g'\) ) (M1)
eg \(h' = fg' + gf'\) , \(h'(3) = f(3) \times g'(3) + g(3) \times f'(3)\)
correct substitution (A1)
eg \(h'(3) = 3( - 3) + ( - 18) \times 1\)
\(h'(3) = - 27\) A1
attempt to find the gradient of the normal (M1)
eg \( - \frac{1}{m}\) , \( - \frac{1}{{27}}x\)
attempt to substitute their coordinates and their normal gradient into the equation of a line (M1)
eg \( - 54 = \frac{1}{{27}}(3) + b\) , \(0 = \frac{1}{{27}}(3) + b\) , \(y + 54 = 27(x - 3)\) , \(y - 54 = \frac{1}{{27}}(x + 3)\)
correct equation in any form A1 N4
eg \(y + 54 = \frac{1}{{27}}(x - 3)\) , \(y = \frac{1}{{27}}x - 54\frac{1}{9}\)
[7 marks]
Examiners report
Nearly all candidates who attempted to answer parts (a) and (c) did so correctly, as these questions simply required them to understand the notation being used and to read the values from the given table.
In part (b), the majority of candidates earned one mark for stating that \(h''(x) = 0\) at point P. As this is not enough to determine a point of inflexion, very few candidates earned full marks on this question.
Nearly all candidates who attempted to answer parts (a) and (c) did so correctly, as these questions simply required them to understand the notation being used and to read the values from the given table.
Part (d) proved to be quite challenging for even the strongest candidates, as almost none of them used the product rule to find \(h'(3)\). The most common error was to say \(h'(3) = f'(3) \times g'(3)\). Despite this error, many candidates were able to earn further method marks for their work in finding the equation of the normal. There were also a small number of candidates who were able to find the equation for \(h'(x)\) , and from that \(h''(x)\). These candidates were often successful in earning full marks, although this method was quite time-consuming.

