| Date | May 2009 | Marks available | 7 | Reference code | 09M.1.sl.TZ1.10 |
| Level | SL only | Paper | 1 | Time zone | TZ1 |
| Command term | Find | Question number | 10 | Adapted from | N/A |
Question
Let \(f(x) = \frac{{ax}}{{{x^2} + 1}}\) , \( - 8 \le x \le 8\) , \(a \in \mathbb{R}\) .The graph of f is shown below.
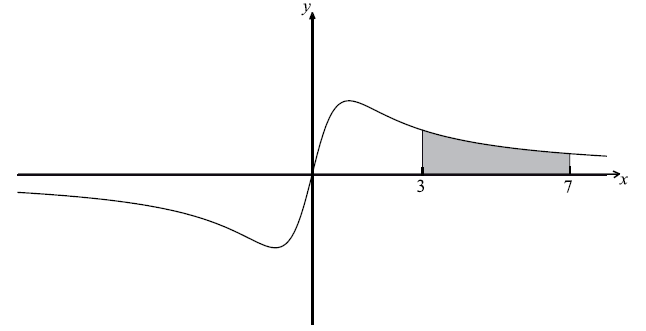
The region between \(x = 3\) and \(x = 7\) is shaded.
Show that \(f( - x) = - f(x)\) .
Given that \(f''(x) = \frac{{2ax({x^2} - 3)}}{{{{({x^2} + 1)}^3}}}\) , find the coordinates of all points of inflexion.
It is given that \(\int {f(x){\rm{d}}x = \frac{a}{2}} \ln ({x^2} + 1) + C\) .
(i) Find the area of the shaded region, giving your answer in the form \(p\ln q\) .
(ii) Find the value of \(\int_4^8 {2f(x - 1){\rm{d}}x} \) .
Markscheme
METHOD 1
evidence of substituting \( - x\) for \(x\) (M1)
\(f( - x) = \frac{{a( - x)}}{{{{( - x)}^2} + 1}}\) A1
\(f( - x) = \frac{{ - ax}}{{{x^2} + 1}}\) \(( = - f(x))\) AG N0
METHOD 2
\(y = - f(x)\) is reflection of \(y = f(x)\) in x axis
and \(y = f( - x)\) is reflection of \(y = f(x)\) in y axis (M1)
sketch showing these are the same A1
\(f( - x) = \frac{{ - ax}}{{{x^2} + 1}}\) \(( = - f(x))\) AG N0
[2 marks]
evidence of appropriate approach (M1)
e.g. \(f''(x) = 0\)
to set the numerator equal to 0 (A1)
e.g. \(2ax({x^2} - 3) = 0\) ; \(({x^2} - 3) = 0\)
(0, 0) , \(\left( {\sqrt 3 ,\frac{{a\sqrt 3 }}{4}} \right)\) , \(\left( { - \sqrt 3 , - \frac{{a\sqrt 3 }}{4}} \right)\) (accept \(x = 0\) , \(y = 0\) etc) A1A1A1A1A1 N5
[7 marks]
(i) correct expression A2
e.g. \(\left[ {\frac{a}{2}\ln ({x^2} + 1)} \right]_3^7\) , \(\frac{a}{2}\ln 50 - \frac{a}{2}\ln 10\) , \(\frac{a}{2}(\ln 50 - \ln 10)\)
area = \(\frac{a}{2}\ln 5\) A1A1 N2
(ii) METHOD 1
recognizing the shift that does not change the area (M1)
e.g. \(\int_4^8 {f(x - 1){\rm{d}}x} = \int_3^7 {f(x){\rm{d}}x} \) , \(\frac{a}{2}\ln 5\)
recognizing that the factor of 2 doubles the area (M1)
e.g. \(\int_4^8 {2f(x - 1){\rm{d}}x = } 2\int_4^8 {f(x - 1){\rm{d}}x} \) \(\left( { = 2\int_3^7 {f(x){\rm{d}}x} } \right)\)
\(\int_4^8 {2f(x - 1){\rm{d}}x = a\ln 5} \) (i.e. \(2 \times \) their answer to (c)(i)) A1 N3
METHOD 2
changing variable
let \(w = x - 1\) , so \(\frac{{{\rm{d}}w}}{{{\rm{d}}x}} = 1\)
\(2\int {f(w){\rm{d}}w = } \frac{{2a}}{2}\ln ({w^2} + 1) + c\) (M1)
substituting correct limits
e.g. \(\left[ {a\ln \left[ {{{(x - 1)}^2} + 1} \right]} \right]_4^8\) , \(\left[ {a\ln ({w^2} + 1)} \right]_3^7\) , \(a\ln 50 - a\ln 10\) (M1)
\(\int_4^8 {2f(x - 1){\rm{d}}x = a\ln 5} \) A1 N3
[7 marks]
Examiners report
Part (a) was achieved by some candidates, although brackets around the \( - x\) were commonly neglected. Some attempted to show the relationship by substituting a specific value for x . This earned no marks as a general argument is required.
Although many recognized the requirement to set the second derivative to zero in (b), a majority neglected to give their answers as ordered pairs, only writing the x-coordinates. Some did not consider the negative root.
For those who found a correct expression in (c)(i), many finished by calculating \(\ln 50 - \ln 10 = \ln 40\) . Few recognized that the translation did not change the area, although some factored the 2 from the integrand, appreciating that the area is double that in (c)(i).

